
Here
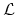
is the operator
and
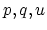
, and
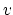
are scalar functions of position,
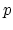
and
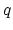
having continuous first derivatives, and
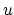
and
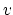
having continuous
second derivatives. The RHS integral over
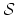
denotes the
surface that encloses the volume
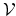
, and
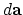
is the
surface element vector pointing in the normal direction. (25 points)
2)
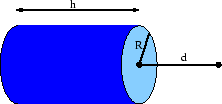
Consider a uniformly charged circular cylindrical shell having
total charge  , radius
, radius  , and height
, and height  . Determine the electric
field and the electric potential
at a point on the axis of the cylinder
a distance
. Determine the electric
field and the electric potential
at a point on the axis of the cylinder
a distance  from the right side of the cylinder, as
shown in Fig. 1. (25 points)
from the right side of the cylinder, as
shown in Fig. 1. (25 points)
Figure 1:
Prob 2
 |
3)
A rectangular pipe, running parallel to the  -axis (from
-axis (from
 to
to  ), has three grounded metal sides, at
), has three grounded metal sides, at  ,
,
 , and
, and  . The fourth side, at
. The fourth side, at  , is maintained at a
specified potential
, is maintained at a
specified potential  (constant). Find the electric potential explicitly.
(25 points)
(constant). Find the electric potential explicitly.
(25 points)
4)
A dielectric sphere with permitivity  and
radius
and
radius  is
embedded in another dielectric material (of infinite size) with
permitivity
is
embedded in another dielectric material (of infinite size) with
permitivity  . Suppose that a point charge of
. Suppose that a point charge of 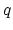 is
embedded at the centre of the sphere and that there is no other
embedded (free) charge. Find the electric displacement, the electric
field, and the electric potential as a function of radius
is
embedded at the centre of the sphere and that there is no other
embedded (free) charge. Find the electric displacement, the electric
field, and the electric potential as a function of radius  from the
centre of the sphere, and calculate the bound surface charge density
at
from the
centre of the sphere, and calculate the bound surface charge density
at  . Assume that both dielectric media have linear response.
See Fig. 2. (25 points)
. Assume that both dielectric media have linear response.
See Fig. 2. (25 points)
Figure 2:
Prob 4
 |


 Next: Solutions
Up: Midterm 1
Previous: Midterm 1
Hyok-Jon Kwon
Next: Solutions
Up: Midterm 1
Previous: Midterm 1
Hyok-Jon Kwon
2001-12-19