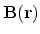 |
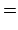 |
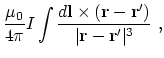 |
(14) |
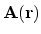 |
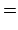 |
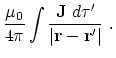 |
(15) |
Using Eq. 5.35 in the textbook, where
 ,
and adding the four sides,
,
and adding the four sides,
 .
.
From the symmetry of the problem,  .
.
2)
Using
 (static case),
(static case),
 , where
, where  is an Amperean loop with a radius
is an Amperean loop with a radius  around the axis of the cylinder. From this, we obtain
around the axis of the cylinder. From this, we obtain  .
.
The magnetic fields are
The surface bound current is linearly related to the discontinuity in
 parallel to the surface at
parallel to the surface at  :
:
 . So
. So
 .
.
3)
The magnetic field at the current loop:
 . The flux:
. The flux:
 . The mutual
inductance is then
. The mutual
inductance is then
 .
.
The emf:
 . So
. So
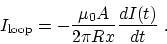 |
(18) |
4)
In the centre of mass frame of the collision, the initial
and the final total momenta must be zero. Therefore, two photons must
be produced in order to conserve momentum.
Since the law of physics is invariant in any reference frame, two
photons are produced in any reference frame.



Next: Final Examination
Up: Midterm 2
Previous: Questions
Hyok-Jon Kwon
2001-12-19


![]() parallel to the surface at
parallel to the surface at ![]() :
:
![]() . So
. So
![]() .
.
![]() . So
. So