Questions

1)

Find the vector potential and the magnetic field at the centre of a square loop, which carries a steady current $I$. Assume that the length of each side of the square is $2a$. (25 points.)

2)

Suppose a long cylindrical permeable material with magnetic permeability $\mu _1$ is embedded in another permeable material with $\mu _2$ of infinite size, and a charge current $I$ flows along the axis of the cylinder. Here the radius of the cylinder is $R$. Assuming that the charge current flows through an infinitesimally thin channel along the axis of the cylinder, find the fields $H$ and $B$ as a function of distance $s$ from the axis of the cylinder. Find also the total surface bound current at $s=R$. (25 points.)

3)

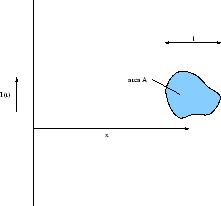
A planar wire loop of arbitrary shape is coplanar with a long, straight wire which carries a current $I(t)$. The loop has a resistance $R$, encloses an area $A$, and is a fixed distance $x$ away from the straight wire. Assume that $x$ is much larger than the characteristic size $l$ of the loop, and assume that the self-inductance of the loop is negligible. Then find the flux through the loop due to the field produced by the straight wire, and therefore find the mutual inductance $M$. Find also the current $I_{\rm loop}$ induced in the loop. (25 points.)

4)

If a particle and an antiparticle (with the same rest mass) collide, they may annihilate each other to generate two photons (quantised light). Explain why this process can NOT generate one photon. (25 points.)

Figure 3: Prob 3