Gauss' Law

9-1

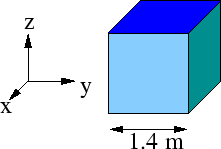
A cube with 1.4 m edges is oriented as shown in Fig. 15 in a region of uniform electric field. Find the electric flux through the right face if the electric field, in Newtons per Coulomb, is given by (a)$6{\bf i}$, (b) $-2{\bf j}$, and (c) $-3{\bf i} + 4{\bf k}$. (d) What is the total flux through the cube for each of these fields?

Figure 15: Prob 9-1

9-2

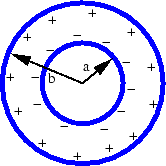
Figure 16 shows a section through two long thin concentric cylinders of radii $a$ and $b$. The cylinders carry equal and opposite charges per unit length $\lambda$. Using Gauss' Law, prove (a) that $E = 0$ for $r < a$ and (b) that between the cylinders $E$ is given by $E={1\over 2\pi \epsilon_0}{\lambda \over r }$.

Figure 16: Prob 9-2

9-3

Two large metal plates of area $1.0 \rm m^2$ face each other. They are 5.0 cm apart and carry equal and opposite charges on their inner surfaces. If $E$ between the plates is 55 N/C, what is the charge on the plates? Neglect edge effects.

9-4

``Gauss' Law for Gravitation'' is

$${1\over 4\pi G}\Phi _g={1\over 4\pi G}\oint {\bf g} \cdot d {\bf A}= -m$$

where $m$ is the enclosed mass and $G$ is the universal gravitation constant. Derive Newton's Law of Gravitation from this. What is the significance of the minus sign?

9-5

A charge of $170 \rm\mu C$ is at the centre of a cube of side 80.0 cm. (a) Find the total flux through each face of the cube. (b) Find the flux through the entire surface of the cube. (c) Would your answers to parts (a) or (b) change if the charge were not at the centre? Explain.

9-6

A solid sphere of radius 40.0 cm has a total positive charge of $26.0 \rm\mu C$ uniformly distributed throughout its volume. Calculate the magnitude of the electric field (a) 0 cm, (b) 10.0 cm, (c) 40.0 cm and (d) 60.0 cm from the centre of the sphere.

9-7

A non-conducting wall carries a uniform charge density of $8.60 \rm\mu C/cm^2$. What is the electric field 7.00 cm in front of the wall? Does your result change as the distance from the wall is varied?

9-8

The starship Voyager travelling through an M-class planet collides with trapped electrons. Since in space there is no ground, the resulting charge build-up can become significant and can damage electronic components, leading to control-circuit upsets and operational anomalies. Model Voyager as a metallic sphere 0.3 km in diameter and assume that it accumulates 0.15 C of charge in one orbital revolution. (a) Find the surface charge density. (b) Calculate the resulting electric field just outside the surface of Voyager.

9-9

Two infinite, nonconducting sheets of charge are parallel to each other. The sheet on the left has a uniform surface charge density $\sigma$, and the one on the right has a uniform charge density $-\sigma$. Calculate the value of the electric field at points (a) to the left of, (b) in between, and (c) to the right of the two sheets.