The Kinetic Theory of Gases

6-1

(a) What is the number of molecules per cubic metre in air at $20 \rm ^o C$ and at pressure of 1.0 atm ( $=1.01\times 10^5  \rm Pa$)? (b) What is the mass of this $1 \rm m^3$ of air ? Assume that 75 % of the molecules are nitrogen ($\rm N_2$) and 25 % oxygen ($\rm O_2$).

6-2

The mass of the $\rm H_2$ molecule is $3.3\times 10^{-24} \rm g$. if $10^{23}$ hydrogen molecules per second strike $2.0 \rm cm^2$ of wall at an angle of $55  \rm ^o$ with the normal when moving with a speed of $1.0\times 10^5 \rm cm/s$, what pressure do they exert on the wall?

6-3

At what temperature is the average translational kinetic energy of a molecule equal to $1.0 \rm eV$? ( $1.0  \rm eV = 1.6\times 10^{-19}  J$).

6-4

A vertical cylinder with a heavy piston contains air at 300 K.The initial pressure is 200 kPa, and the initial volume is $0.350  \rm m^3$. Take the molar mass of air as $28.9 \rm g/mol$ and assume that $C_V =5R//2$. (a) Find the specific heat of air at constant volume in units of $\rm J/kg\cdot C$. (b) calculate the mass of the air in the cylinder. (c) suppose the piston is held fixed. Find the energy input required to raise the temperature of the air to 700 K. (d) Assume again the condition of the initial state and that the heavy piston is free to move. Find the energy input required to raise temperature to 700 K.

6-5

A mass of gas occupies a volume of 4.3 L at a pressure of 1.2 atm and a temperature of 310 K. It is compressed adiabatically to a volume of 0.76 L. Determine (a) the final pressure and (b) the final temperature, assuming it to be an ideal gas for which $\gamma = 1.4$. ( Hint: it is not necessary to make any unit conversions.)

6-6

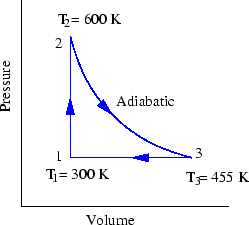
A reversible heat engine carries 1.00 mol of an ideal monatomic gas around the cycle shown in Fig. 10. Process $1\rightarrow 2$ takes place at constant volume, process $2\rightarrow 3$ is adiabatic, and process $3\rightarrow 1$ takes place at a constant pressure. (a) Compute the heat $Q$, the change in internal energy $\Delta U$, and the work done $W$, for each of the three processes and for the cycle as a whole. (b) If the initial pressure at point 1 is 1.0 atm, find the pressure and the volume at points 2 and 3.

Figure 10: Prob 6-6

6-7

The escape speeds from the surface of the earth and the moon are respectively 11.2 km/s and 2.3 km/s. (a) Compute the temperatures at which the rms speed is equal to the speed of escape from the surface of the earth for molecular oxygen. (b) Do the same for the moon. (c) The temperature high in the earth's upper atmosphere is about 1000 K. Would you expect to find much hydrogen there? Much oxygen?

6-8

At 273 K and $1.00\times 10^{-2}  \rm atm$ the density of a gas is $1.24 \times 10^{-5} \rm g/cm^3$. (a) Find $v_{\rm rms}$ for the gas molecules. (b) Find the molecular mass of the gas and identify it.