Addition to Einstein

Einstein formulated his special relativity in 1905. One hundred years later, in 2005, he came to me and asked me what I have done to make him happy. I told him I constructed a webpage dedicated to him.

• I then asked him what he discussed with Bohr when he met him. Bohr was interested in the electron orbit of the hydrogen atom. Then I asked him whether they discussed how the orbit looks to moving observers. He told me he has no recollection of talking about this problem. At that time, the moving hydrogen atom (with a relativistic speed) was beyond the scope of physics. Even these days, it is not possible to accelerate the hydrogen atom.

• The hydrogen atom played a pivotal role during the transition from classical mechanics to quantum mechanics where the bound-state orbits are replaced by standing waves.

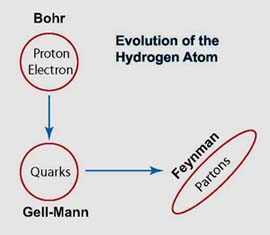
• In 1964, Murray Gell-Mann formulated the quark model where the proton became a quantum bound state of more fundamental particles called the quarks. Unlike the hydrogen atom. the proton can be accelerated, and its speed can become as close as that of light. Then the proton does not appear like a bound state. Indeed, in 1969, Richard Feynman observed this phenomenon systematically and came up with his parton picture.

  The original hydrogen problem of Bohr and Einstein thus becomes that of whether the parton model is a Lorentz-boosted quark model. Click here for a detailed story.

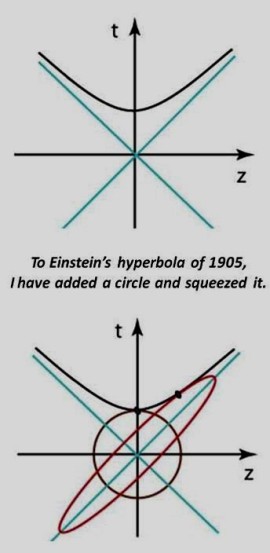
  I learned the mathematics of these figures during my high-school years (1951-54), even though I did not know they have anything to do with Einstein.

• Einstein told me the quarks and partons are very strange to him. He asked to explain in terms of the language he could understand. I then showed this figure consisting of a hyperbola, circle, and ellipse.
  1. He was able to recognize the hyperbola shown in the figure. There is an invariant quantity when we move along this hyperbola. For example, the particle mass is a Lorentz-invariant quantity.

  2. I told him I added a circle tangent to the hyperbola. As the tangential point moves along the hyperbola, the circle becomes squeezed into an ellipse. The area of the ellipse remains constant.

     As the tangential point moves far away from the center, the ellipse becomes concentrated into the line which makes the 45^o angle between the horizontal and vertical axes.

     In terms of the language of physics, the circle and the the narrow ellipse correspond to the quark and parton models respectively. Click here for the physics story.

• Einstein said the mathematics of the circle and ellipse is very easy to understand, but he asked me whether I did all the physics alone. I said No. I organized earlier works of Dirac, Wigner, and Feynman. I showed this table of organization.

  I had a photo with Dirac's bust at the Fine Hall Library (for physics and math) of Princeton University (2013).

  1. Among those, Paul A. M. Dirac was most inspirational to me. I then told him this story to Einstein, and asked him whether he met Dirac. He said Dirac was a young man from England, and he once met Dirac at the 1927 Solvay conference.

  2. It is possible to integrate the works of Dirac, Wigner, and Feynman to obtain the Bohr-Einstein picture of moving bound states. Click here for this work as a an extension of Einstein's E = mc^{2 .}

  3. I did not have to invent new mathematics. The mathematical framework was based on what I learned during my high-school years (1961-54).

• Click here for more about Einstein.