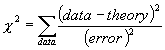
We expect a “good” value of c2 to be about the number of data points, or, better yet, the number of degrees of freedom (dof) = data points – parameters in the theory. Reduced c2 has the #dof divided out, so we expect a reasonable value to be about 1. The procedure of fitting data to a theory is to minimize c2 with respect to the parameter in the theory. When the theory has only a linear dependence on its parameters, then the minimum in c2 can be determined analytically. This is why it’s very nice to put data into a form where it can be described by a theory that depends linearly on its parameters. is linear in the parameters (A,B,C,…). So let’s minimize c2 for a simple polynomial: a straight line theory.