For the graphs shown below, the horizontal axis represents the time. The vertical axis is unspecified.

Your roommate peeks over your shoulder while you are reading a physics text* and notices the following sentence: "In free-fall the acceleration is always g and always straight downward regardless of the motion." Your roommate finds this peculiar and raises three objections:
* Physics, by E. Hecht (Brooks Cole Publishers, 1994)
| A ball is launched up a ramp by a spring as shown in the figure at the right. At the time when the clock starts, the ball is near the bottom of the ramp and rolling up the ramp as shown. It goes to the top and then rolls back down. For the graphs shown below, the horizontal axis represents the time. The vertical axis is unspecified. |
 |
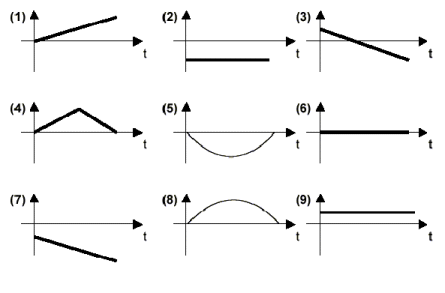
| (a) The x component of the ball's position. | _______ |
| (b) The y-component of the ball's velocity | _______ |
| (c) The x-component of the ball's acceleration | _______ |
| (d) The y-component of the normal force the ramp exerts on the ball | _______ |
| (e) The x-component of the ball's velocity | _______ |
| (f) The x-component of the force of gravity acting on the ball | _______ |
|
An old Yiddish joke is told about a farmer in Chelm, a town famous for the lack of wisdom of its inhabitants. One day the farmer was going to the mill to have a bag of wheat ground into flour. He was riding to the mill on his donkey, with the sack of wheat thrown over the donkey's back behind him. On his way, he met a friend. His friend chastised him. "Look at you! You must weigh 200 pounds and that sack of flour must weigh 100. That's a very small donkey! Together, you're too much weight for him to carry!" On his way to the mill the farmer thought about what his friend had said. On his way home, he passed his friend again, confident that this time the friend would be satisfied. The farmer still rode the donkey, but this time he carried the 100 pound bag of flour on his own shoulder!
|
|
| The figure at the right shows a multiple-exposure photograph of a ball rolling up an inclined plane. (The ball is rolling in the dark, the camera lens is held open, and a brief flash occurs every 3/4 sec four times.) The left-most ball corresponds to an instant just after the ball was released. The right-most ball is at the highest point the ball reaches. | 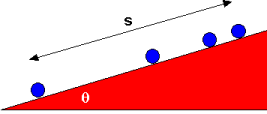 |
| George left the lights in his truck on while in a truck stop in Kansas and his battery went dead. Fortunately, his friend Al was there. Unfortunately, Al was driving his Geo Metro. Fortunately, the road was very flat. George was able to convince Al to give his truck a long slow push to get it up to 20 miles/hour. At this speed, George can let in the truck's clutch and the truck's engine should start up. |  |
| A popgun is angled so that it shoots a small dense ball through the air as shown in the figure.
| 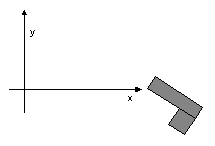 |
| For the graphs shown at the right, the horizontal axis represents the time. The vertical axis is unspecified. For each of the following quantities, select the letter of the graph that could provide a correct graph of the quantity for the ball in the situation shown (if the vertical axis were assigned the proper units). Use the x and y coordinates shown in the picture. If none of the graphs could work write N. The time graphs begin just after the ball leaves the gun.
|
 |
| In class we did a demonstration in which two objects of different masses were dropped, one straight down, and the other shot off to the side by a spring. Both objects seemed to hit the ground at about the same time. Explain why this happens in terms of the physics we have learned. Does it matter how fast we shoot the one launched sideways? | 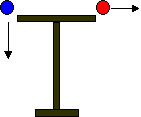 |