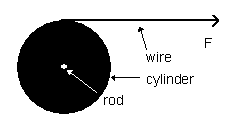
Wire is often delivered wrapped on a large cylindrical spool. Suppose such a spool is supported by resting on a horizontal metal rod that is pushed through a hole that runs through the center of the spool. A worker is pulling some wire off the spool by exerting a force on it something like is shown in the diagram at the right. (If you have ever bought wire in a hardware store, this is the way they usually store and dispense it.)

Suppose the spool rotates on the rod essentially without friction. The spool is approximately a uniform cylinder with a mass of 50 kg and a radius of 30 cm. The worker pulls on the wire for 2 seconds with a force of 30 Newtons. At the end of the 2 seconds he immediately clamps on a brake which very quickly stops the spool's rotation. Just before he put the brake on, how fast was the spool rotating? How much wire did he pull off the spool?

Solution

The spool is accelerated by a constant torque. We need to first find out the acceleration so we can figure out the average angular velocity. This will in turn tell us how much the spool rotated in that time. The equation relating angular acceleration and unbalanced torque is

where α is the angular acceleration, α = Δω/Δt, τ is the torque, and I is the moment of inertia. In this case, we are approximating the spool as a uniform cylinder, so its moment of inertia is

The torque is

The result is that the angular acceleration is

(We put in the radians because that is the dimensionless angular variable we know we get when we use these equations.)

From the acceleration we can get the change in the angular velocity.

Since the initial angular velocity is 0,

This is how fast the spool was rotating just before he put the brake on. Now we can use the definition of the average angular velocity to get the total angle rotated, Δθ.

Since the wire rolled off the spool, what we want is the arc length corresponding to this angle. By the definition of radians this is just

Solution (the images were unavailable at the time of writing and will be supplied asap)

In order for an extended object to remain stationary (or to move at a constant velocity without rotating), two conditions have to be satisfied. For the center of mass to be not accelerating, by Newton's second law, the vector net force must be zero. For the object not to be rotating, the net torque must be zero. For an object whose motion can be considered as moving in two dimensions (a plane), a convenient way to represent these conditions is as follows.

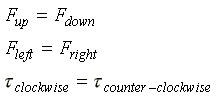
To analyze the motion of the ladder, lets assume the men (M1 on the left, M2 on the right) are carrying the ladder along at a constant velocity. Then all the above conditions must be satisfied. To apply, them, we need to construct an extended free-body diagram. This is shown below.

There are no left-right forces, so we only have to balance the up-down forces and the torques. The up-down balance equation is:

Since we know by analyzing the up-down forces on the cat and using Newton's 1st and 3rd laws that the normal force the cat exerts on the ladder is equal to the cat's weight, we can simplify the notation for this equation and write:

[1]

To calculate the torque balance, let's choose the pivot point to be at the point where the man on the left is holding the ladder. Then the man on the right's force produces a counter-clockwise torque and the two weights produce a clockwise torque. Since the man on the left is exerting his force at the pivot, his force produces no torque. The resulting equation is:

[2]

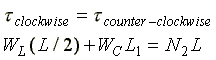
Is this enough? We know the masses of the ladder and the cat, so we can find their weights (W_L, W_C). We know the length of the ladder (L), and the position of the cat (L₁). What we don't know are the forces exerted by the men. We therefore have two unknowns (N₁, N₂) and two equations ([1] and [2]) so we should be OK. Eq. [1], the up-down force equation, has both unknowns in it. Eq. [2], the torque equation, has only one of them. So we can solve [2] for N₂, then put the result into [1] and solve for N₁. This favorable situation happened because we were clever enough to choose the pivot point of the torque equation at the application point of one of the unknown forces, so it disappeared from that equation (because it was multiplied by its distance from the pivot, 0). If we had chosen the pivot at the "natural" point -- the center of mass of the ladder -- we would have had to solve two equations in two unknowns where both unknowns appeared in both equations. Not too bad, but not as quick or convenient as the choice we made. Here are the solutions.

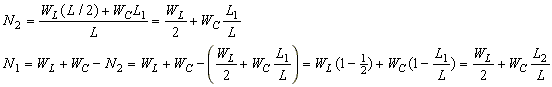
I've written L₂ for L-L₁ so you can see the symmetry of the answers for the two forces. Each man shares half the weight of the ladder and they share the weight of the cat in proportion to the fraction of the ladder's length the cat is away from the other man. When the cat is right at one of the men, that man carries all of the cat's weight and the other man none of it. This makes good intuitive sense.

We can put the numbers in now. The ladders weight is (15 kg)(10 N/kg) = 150 N. The cat's weight is (5 kg)(10 N/kg) = 50 N. The distance the cat is from man 1 is L₁=5 m, and the distance the cat is from man 2 is L₂=1 m. Putting these in gives:

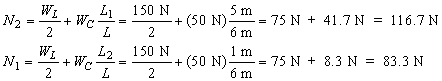
Solution

We assume that the melt-water would form a thin shell of mass m = 2.3 × 10¹⁹ kg and radius R_E = 6.38 × 10⁶ m around the Earth. This shell would increase Earth's moment of inertia by an amount Δl = ²/₃mR_E². If we treat Earth as a uniform solid sphere, this would represent a fractional increase of   ^ΔI/_I0 = (5/3)(m/M_E). Thus, the fractional increase in the moment of inertial would be on the order of   ^1019kg/_10²⁴kg = 10^-6. In this process, angular momentum would be conserved, so the quantity Iω = I (^2π/_T), where T is the rotation period or length of a day, must remain constant. Therefore, the length of the day must also experience a fractional increase on the order of 10^-6. This would give an increase in the length of the day of   ΔT ~ 10^-6 T₀ = 10^-6(86400 s) = 0.0864 s, or   ΔT ~ 0.1s.