| Homework due Oct 20 | Name: | Section: |
14. Stopping a train
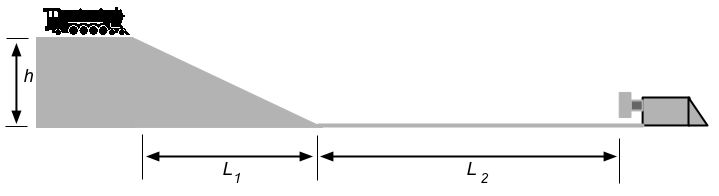
A toy train of mass m comes off a hill traveling at a velocity v0, rolls down an incline of height h, rolls a short distance on a straight track, and strikes a bumper containing a spring of spring constant k. The distances are as indicated on the figure below. The train is just rolling, not powered.
- Assuming that friction and the rotational energy of the wheels can be ignored, describe the changes in the forms of energy of the system starting with the instant the train begins down the hill until it comes to a stop at the bumper.
- What is the speed of the train, v, when it is on the straight piece of track? Express your answer in terms of the symbols given above
Note to the instructor: This problem is stated as it is in order to address three issues. 1. Students often fail to think about the time structure of a problem, and don't have a "mental movie" where they can watch what's happening and think about what's happening to the various physical variables. 2. Students sometimes focus on the changes in each kind of energy but don't thing about the fact that the changes are transformations from one kind to another and the changes compensate, leaving the totals the same. 3. Students often are uncomfortable with symbols and want to put in number right away. When they do this, they fail to learn to work with symbols. By not giving any numbers we are requiring them to begin to develop a valuable skill.
15. Adjusting a Projectile
Two high school students in a physics olympics competition are trying to hit a small box on the floor using a spring-loaded marble gun placed horizontally on and fastened rigidly to a table. The first student compresses the spring 1.0 cm and the marble falls 20 cm short of the target which is 2.0 m horizontally from the edge of the table. How far should the second student compress the spring so that the same marble falls into the box?
Note to the instructor: This is a combination problem -- best done by combining energy concepts with the standard projectile motion. The "correction" gives the problem a different twist.The student has to decide what is known and what has to be figured out -- and it has to be done twice with different results.
16. Rolling carts down hill
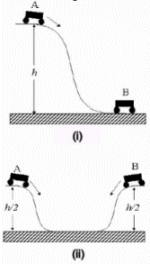
| Two carts A and B are identical in all respects. They roll down a hill and collide as shown in the figures at the right.
Figure (i): Cart A starts from rest on a hill at a height h above the ground. It rolls down and collides head-on with cart B which is initially at rest on the ground. The two carts stick together.
Figure (ii): Carts A and B are at rest on opposite hills at heights h/2 above the ground. They roll down, collide head-on with each other
on the ground and stick together.
Which of the following statements are true about the two-cart system just before the carts collide in the two cases? By putting × in the appropriate figure column, give all the statements that are true. If none are true, write N. |
 |
| Figure (i) | Figure (ii) |
- The kinetic energy of the system is zero in case (ii).
- The kinetic energy of the system is greater in case (i) than in case (ii).
- The kinetic energy of the system is the same in both cases.
- The total momentum of the system is greater in case (ii) than in case (i).
- The total momentum of the system is the same in both cases.
|
17. Blood Pressure
The human heart has to pump the average adult's 6.0 L of blood through the body every minute. The heart must do work to overcome frictional forces that resist the blood flow. The average blood pressure is 1.3×104 N/mē.
- Compute the work done moving the 6.0 L of blood completely through the body, assuming the blood pressure always takes its average value.
- What power output must the heart have to do this task once a minute?
Hint: When the heart contracts, it applies force to the blood. Pressure is just force/area, so we can write
work = (pressure)(area)(distance)
But (area)(distance) is just the bood volume passung through the heart.