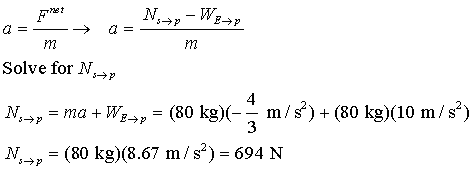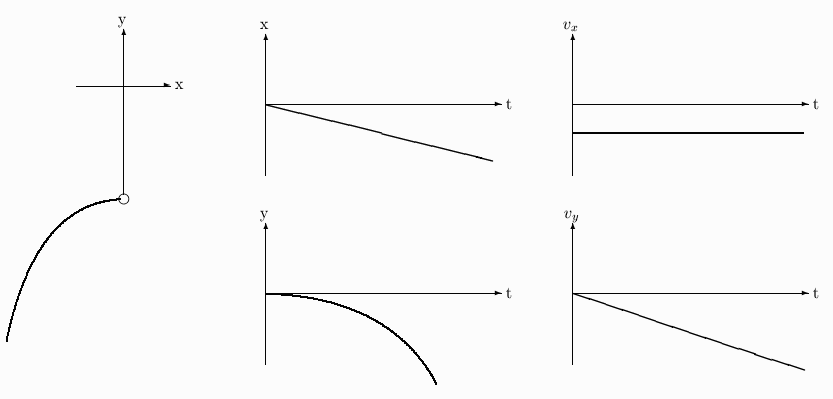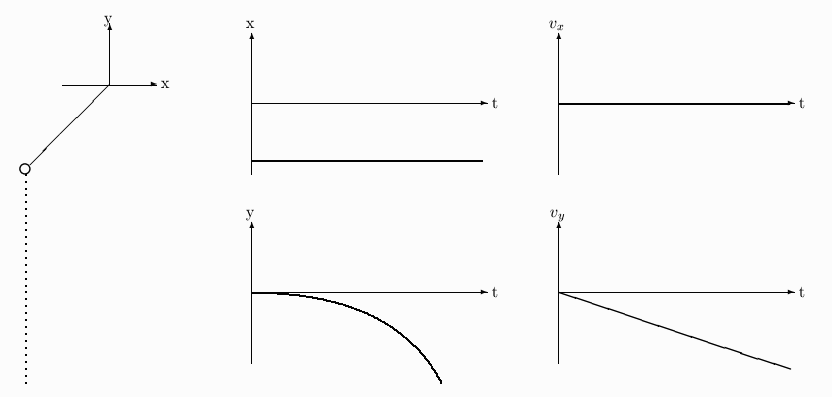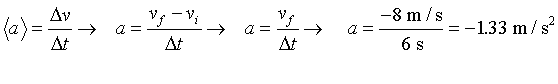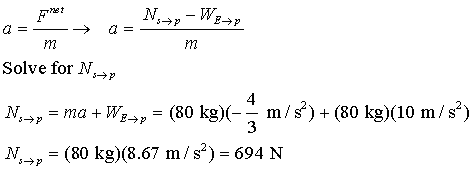A pendulum with a ball at the end is set swinging by holding it at the point marked A in the figure and releasing it. The x and y coordinate are shown with the origin at the crossing point of the axes and the positive directions indicated by the arrowheads. (a) During one swing, the string breaks exactly at the bottom-most point of the swing (the point labeled B in the figure) as the ball is moving from A to B towards C. Using solid lines sketch on the figure the path of the ball after the string has broken and sketch qualitatively the x and y coordinates of the ball and the x and y components of its velocity on the graphs at the right. Take t=0 to be the instant the string breaks.

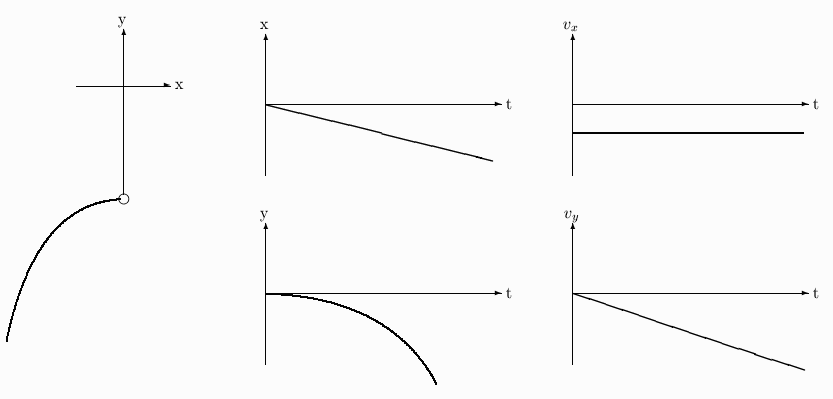
(b) During a second trial, the string breaks again, but this time at the top-most point of the swing (the point labeled C in the figure). Using dashed lines sketch on the figure the path of the ball after the string has broken and sketch qualitatively the x and y coordinates of the ball and the x and y components of its velocity on the graphs at the right. Take t=0 to be the instant the string breaks.

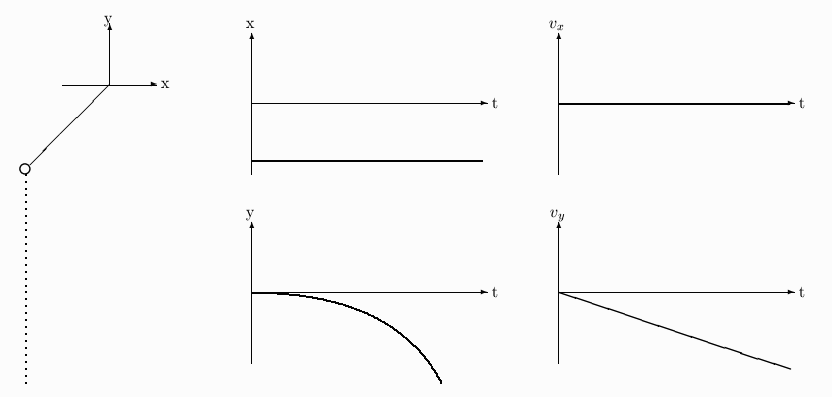
Both graphs of y vs t should be shifted down to start at a negative y-value, since the ball starts out below the x-axis.

A passenger is standing on a scale in an elevator. The building has a height of 500 feet, the passenger has a mass of 80 kg, and the scale has a mass of 7 kg. The scale sits on the floor of the elevator. You may take g = 10 N/kg.

(a) Draw free-body diagrams for the passenger and the scale while the scale is sitting at rest on the 33rd floor. Somewhere in your diagram or labeling be sure to identify: (1) the type of force, (2) the object causing the force, and (3) the object feeling the force. Indicate which (if any) two individual forces in these diagrams have the same magnitude.

(b) The elevator now begins to descend. Starting from rest, it takes the elevator 6 seconds to get up to its downward speed of 8 m/s. Assuming that it is accelerating downward at a uniform rate during these 6 seconds, which of the forces in your diagram for (a) will change? For each force that changes, specify whether it will become bigger or smaller.

(c) While it is accelerating downward, which of the forces in your diagrams have the same magnitude? For each equality you claim, explain why you think they are equal.

(d) While it is accelerating downward, what does the scale read?

Solution

(a) Since the passenger is not accelerating, the two forces acting on him must be equal and opposite by N1. That is, the passenger's weight equals the upward (normal) force from the scale: N_{scale->passenger} = - W_{earth->passenger}. By N3, any pair of forces with their labels reversed -- two forces objects exert reciprocally on each other -- must be equal and opposite. Therefore N_{scale->passenger} = N_{passenger -> scale}. The sum of the two downward forces on the scale is also equal to the upward force on the scale, but that wasn't asked for.

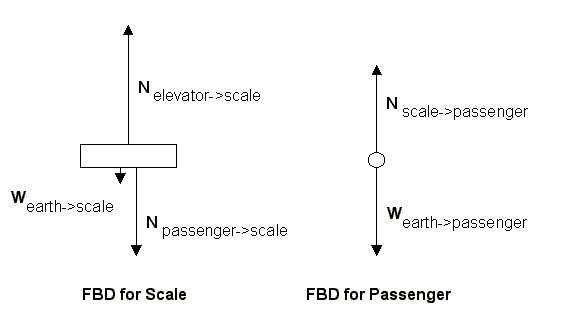
(b) The only forces in the diagram that can change are the normal forces. We know that the weights don't change, no matter how an object moves (unless it moves far from the earth's surface). If the elevator is accelerating downward, it is trying to move away from the scale. So the normal force the elevator exerts on the scale will be reduced. Since the scale is trying to move away from the passenger, the normal forces between the two of them will also be reduced.

(c) When an object is accelerating, we can't apply N1 but N3 always applies no matter how the objects are moving. Therefore, now only the normal forces of the scale on the passenger and the passenger on the scale will still be equal.

(d) The scale reads whatever normal force it is exerting since that tells how much its spring is being squeezed. Therefore the value will be N_{scale->passenger} = N_{passenger -> scale}. The latter is the easiest to calculate from a = F^net/m. Since we know the motion of the passenger (assuming he stays on the scale), we should be able to get a. We also know m and one of the forces (the passenger's weight). There should therefore be only one unknown in our equation and we should be able to solve for it. Let's start by finding a.

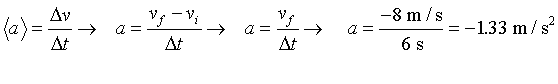
Now we can figure out the normal force.