| Homework due Sept. 29 |
Name: |
Section: |
9. The farmer and the donkey
An old Yiddish joke is told about a farmer in Chelm, a town famous for the lack of wisdom of its inhabitants. One day the farmer was going to the mill to have a bag of wheat ground into flour. He was riding to the mill on his donkey, with the sack of wheat thrown over the donkey's back behind him. On his way, he met a friend. His friend chastised him. "Look at you! You must weigh 200 pounds and that sack of flour must weigh 100. That's a very small donkey! Together, you're too much weight for him to carry!" On his way to the mill the farmer thought about what his friend had said. On his way home, he passed his friend again, confident that this time the friend would be satisfied. The farmer still rode the donkey, but this time he carried the 100 pound bag of flour on his own shoulder!
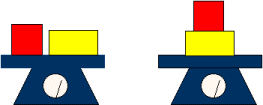 Our common sense and intuitions seem to suggest that it doesn't matter how you arrange things, they'll weigh the same. Let's be certain that the Newtonian framework we are developing yields our intuitive result. Analyze the problem by considering the following simplified picture: two blocks resting on a scale. One block weighs 10 N, the other 25 N. In case 1 the blocks are arranged on the scale as shown in the figure on the left. In case 2 the blocks are arranged as shown on the right. Each system has come to rest. Analyze the forces on the blocks and on the scale in the two cases by isolating the objects -- each block and the scale -- and using Newton's laws, show that according to the principles of Newton's laws, the total force exerted on the scale by both blocks together must be the same in both cases. (Note: It's not enough to say: "They have to be the same." That's just restating your intuition. We need to see that reasoning using only the principles of our Newtonian framework leads to the same conclusion.)
Our common sense and intuitions seem to suggest that it doesn't matter how you arrange things, they'll weigh the same. Let's be certain that the Newtonian framework we are developing yields our intuitive result. Analyze the problem by considering the following simplified picture: two blocks resting on a scale. One block weighs 10 N, the other 25 N. In case 1 the blocks are arranged on the scale as shown in the figure on the left. In case 2 the blocks are arranged as shown on the right. Each system has come to rest. Analyze the forces on the blocks and on the scale in the two cases by isolating the objects -- each block and the scale -- and using Newton's laws, show that according to the principles of Newton's laws, the total force exerted on the scale by both blocks together must be the same in both cases. (Note: It's not enough to say: "They have to be the same." That's just restating your intuition. We need to see that reasoning using only the principles of our Newtonian framework leads to the same conclusion.)
Solution
If we isolate each block and the scale and consider the forces acting on them individually (as N0 tells us to), we get the following diagrams and forces. (The scale is calibrated so as to show 0 when nothing is on it. This means we don't need to include the scale's weight. It is only the squeezing force above that amount that is measured.)
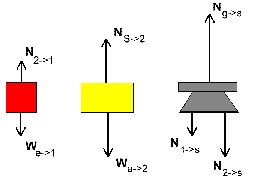
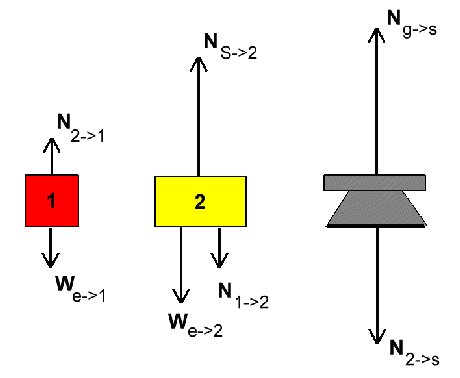
On the left we show what happens when the boxes are sitting next to each other on the scale. In each case, we
- Isolate each object.
- Determine the forces each object feels, specifying what kind of force it is and who is causing it. Here, we start with gravity (the object's weight) and add appropriate forces for everything that is touching it.
- On the object we balance the forces according to N2: a = Fnet/m. If the object is not accelerating, this means acceleration is zero so all the forces the object feels must cancel. (NOT žall the forces on the object are zeroÓ.)
- We then look for pairing between objects in pairs with indices like FA->B = - FB->A.
.
In this case, all forces are up or down. (None to the side or at an angle.) So instead of working with vectors, we can use magnitudes and say that for each object all the up forces must balance all the down forces. For the case on the left and right this gives us the equations (on left and right respectively):
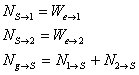
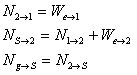 Now if we use N3, we see on the left that
Now if we use N3, we see on the left that
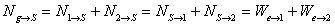
while on the right
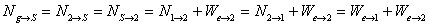
In both cases we chain back and forth using N2 and N3 and can show we get the same result.
10. Ball on a ramp
|
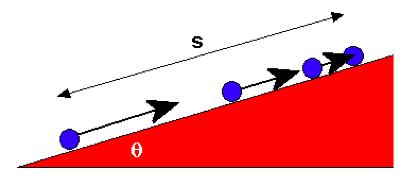
The figure at the right shows a multiple-exposure photograph of a ball rolling up an inclined plane. (The ball is rolling in the dark, the camera lens is held open, and a brief flash occurs every 3/4 sec four times.) The left-most ball corresponds to an instant just after the ball was released. The right-most ball is at the highest point the ball reaches. | 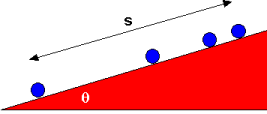 |
- Copy this picture on your paper and, at each ball, draw an arrow to indicate the velocity of the ball at the instant when it was at that point in space. Explain what is happening ("tell the story" of the picture).
- For the instant of time when the ball is at the second position shown from the left, draw a free-body diagram for the ball and indicate all forces acting on it.
- If your force diagram doesn't include an arrow pointing up the ramp, explain why the ball keeps rolling up the ramp.
- If the mass of the ball is m, what is its acceleration?
- If the angle θ is equal to 30o, how long is the distance s?
Solution
(a) In the first picture the ball is moving upward with a large speed. As it goes up, it slows down, so each arrow is smaller as one goes up. At the topmost point, the ball is turning around -- switching from a positive velocity to a negative velocity -- so at that instant the velocity is zero.
| (b) The ball is only touching the inclined plane (ignoring the air), so the only touching force on it is from the inclined plane. If the ball is rolling, the friction between the plane and the ball is probably very small, so we only need to draw the normal force. The only non-touching force is gravity, which acts down towards the center of the earth, as usual. | 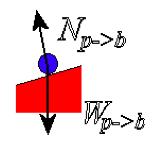 |
(c) It keeps rolling up the ramp because it is rolling up the ramp. That is, by Newton's 1st law, an object doesn't need a force to keep going with a constant velocity. By Newton's 2nd law, the result of forces is to change its velocity. So the net force down the ramp means that if it starts heading up the ramp, the force down will reduce that velocity a bit at a time, but it will keep going up the ramp until the force brings its velocity down to zero. Then the force will succeed in getting it to roll down the ramp.
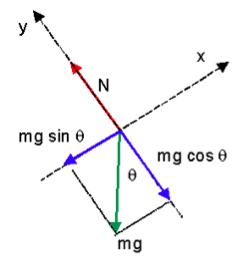 (d) To get this we have to use a = Fnet/m so we need to add all the forces. The forces aren't in the same direction so we're going to have to use vector algebra to figure the sum of them out. A good way to do it is to decompose one of the vectors into two in a convenient way. (This means we "make change" -- replace one vector by two that have the same sum but are more convenient to work with.) Let's choose our coordinates so that x runs along and up the plane and y is perpendicular to it. Then the normal force, N (the red vector), is along the y-axis. We can replace the weight of the ball, W = mg (the green vector), which points straight down, by its x and y component vectors (shown in blue). The sum of the two blue vectors is equal to the green vector, so we can eliminate the green vector and use the two blues instead.
(d) To get this we have to use a = Fnet/m so we need to add all the forces. The forces aren't in the same direction so we're going to have to use vector algebra to figure the sum of them out. A good way to do it is to decompose one of the vectors into two in a convenient way. (This means we "make change" -- replace one vector by two that have the same sum but are more convenient to work with.) Let's choose our coordinates so that x runs along and up the plane and y is perpendicular to it. Then the normal force, N (the red vector), is along the y-axis. We can replace the weight of the ball, W = mg (the green vector), which points straight down, by its x and y component vectors (shown in blue). The sum of the two blue vectors is equal to the green vector, so we can eliminate the green vector and use the two blues instead.
Since we know the ball stays on the plane, the normal force and the y component of the weight must cancel. This leaves only the blue vector pointing down the plane to be our entire net force. It has a magnitude mg sin θ. The acceleration is this net force divided by m to give g sin θ.
(e) Since we now know the acceleration and time and the final velocity (0) we can get the initial velocity v = (2s g sinθ)Ĺ.
11. Shoot and drop
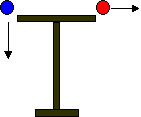
| In class we did a demonstration in which two objects of different masses were dropped, one straight down, and the other shot off to the side by a spring. Both objects seemed to hit the ground at about the same time. Explain why this happens in terms of the physics we have learned. Does it matter how fast we shoot the one launched sideways? |
 |
Solution
Your answer should mention that the horizontal and vertical motion are independent. So the horizontal speed of the the mass does not matter for it vertical motion.
 Our common sense and intuitions seem to suggest that it doesn't matter how you arrange things, they'll weigh the same. Let's be certain that the Newtonian framework we are developing yields our intuitive result. Analyze the problem by considering the following simplified picture: two blocks resting on a scale. One block weighs 10 N, the other 25 N. In case 1 the blocks are arranged on the scale as shown in the figure on the left. In case 2 the blocks are arranged as shown on the right. Each system has come to rest. Analyze the forces on the blocks and on the scale in the two cases by isolating the objects -- each block and the scale -- and using Newton's laws, show that according to the principles of Newton's laws, the total force exerted on the scale by both blocks together must be the same in both cases. (Note: It's not enough to say: "They have to be the same." That's just restating your intuition. We need to see that reasoning using only the principles of our Newtonian framework leads to the same conclusion.)
Our common sense and intuitions seem to suggest that it doesn't matter how you arrange things, they'll weigh the same. Let's be certain that the Newtonian framework we are developing yields our intuitive result. Analyze the problem by considering the following simplified picture: two blocks resting on a scale. One block weighs 10 N, the other 25 N. In case 1 the blocks are arranged on the scale as shown in the figure on the left. In case 2 the blocks are arranged as shown on the right. Each system has come to rest. Analyze the forces on the blocks and on the scale in the two cases by isolating the objects -- each block and the scale -- and using Newton's laws, show that according to the principles of Newton's laws, the total force exerted on the scale by both blocks together must be the same in both cases. (Note: It's not enough to say: "They have to be the same." That's just restating your intuition. We need to see that reasoning using only the principles of our Newtonian framework leads to the same conclusion.)

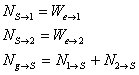
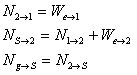


 (d) To get this we have to use a = Fnet/m so we need to add all the forces. The forces aren't in the same direction so we're going to have to use vector algebra to figure the sum of them out. A good way to do it is to decompose one of the vectors into two in a convenient way. (This means we "make change" -- replace one vector by two that have the same sum but are more convenient to work with.) Let's choose our coordinates so that x runs along and up the plane and y is perpendicular to it. Then the normal force, N (the red vector), is along the y-axis. We can replace the weight of the ball, W = mg (the green vector), which points straight down, by its x and y component vectors (shown in blue). The sum of the two blue vectors is equal to the green vector, so we can eliminate the green vector and use the two blues instead.
(d) To get this we have to use a = Fnet/m so we need to add all the forces. The forces aren't in the same direction so we're going to have to use vector algebra to figure the sum of them out. A good way to do it is to decompose one of the vectors into two in a convenient way. (This means we "make change" -- replace one vector by two that have the same sum but are more convenient to work with.) Let's choose our coordinates so that x runs along and up the plane and y is perpendicular to it. Then the normal force, N (the red vector), is along the y-axis. We can replace the weight of the ball, W = mg (the green vector), which points straight down, by its x and y component vectors (shown in blue). The sum of the two blue vectors is equal to the green vector, so we can eliminate the green vector and use the two blues instead.
