
A New Model Course in Applied
Quantum Physics
E.F. Redish,
R.N. Steinberg, M.C. Wittmann
Home | Overview | How Students Learn | Classroom materials | Teacher's Guide
 |
A New Model Course in Applied
Quantum Physics Home | Overview | How Students Learn | Classroom materials | Teacher's Guide |
In teaching mathematics or science, understanding how to incorporate instructional technology and evaluate its impact is of great importance. In this paper, we report on how we are using physics education research both as a guide to the way we develop computer-based curriculum and as a means of assessment. The context of our study is modern physics, which is a subject being taught in a growing number of classes from high school through graduate school. We focus on a computer tutorial on the photoelectric effect and its implementation in a university modern physics course for engineers and scientists.
INTRODUCTION
Physics Education Research
Simulations, computer-based experiments, and digitized
videos are changing the way physics is taught. The developers
of these instructional tools are usually (although not universally)
experts in the subject matter who think carefully about the physics.
The need for a thorough understanding of the subject matter is
obvious. However, a growing number of developers are also recognizing
the importance of applying the techniques of physics education
research (e.g., Thornton & Sokoloff, 1990; Grayson, 1996;
Laws, 1997). In this approach, curriculum development is based
on the systematically measured needs of students and there is
an evaluation and modification of the curriculum based on careful
observations of what real students do in real classrooms (Redish
& Steinberg, 1999; McDermott & Redish, 1999).
Why Modern Physics
Understanding modern physics is of growing importance,
not just to future physicists, but to future engineers, chemists,
and biologists. Fields in which understanding modern physics is
important include photonics, mesoscopic engineering, and medical
diagnostics based on quantum probes. It is therefore not surprising
that modern physics is being taught more often to more students
starting as early as high school.
However, many topics in modern physics are difficult and abstract, and there has been little success in teaching them to all but the strongest students. At the University of Maryland, we are designing a new modern physics / quantum mechanics course that is intended to be accessible to a much wider range of students.1 Our instruction focuses on devices such as LEDís, transistors, and spectrometers. In order to match the instruction to the needs of the students, we are using physics education research as a guide to the development of the curriculum and instructional strategies. Because many of the topics are abstract and do not have easily available hands-on instructional aids, we are using the computer as a tool throughout the course.
Overview of Paper
In this paper, we focus on the photoelectric effect. Understanding
the photoelectric experiment is critical to the development of
the photon model of light, which is prerequisite to the study
of many other topics including the interaction of light and matter,
atomic energy levels, and lasers.
In the next section, we summarize our research on student understanding of the photoelectric effect and the development of an interactive computer program called Photoelectric Tutor (Oberem & Steinberg, 1999). Then we give an overview of the program and describe how its design is based on the findings of the research. We describe how the program is used to improve our understanding of how students learn the photoelectric effect and describe the results of the programís implementation, with particular reference to a university course composed mostly of junior engineering majors. Finally, we briefly describe other examples of how we are using research to develop modern physics computer-based instructional materials.
PHYSICS EDUCATION RESEARCH AND THE PHOTOELECTRIC EFFECT
As part of a study at the University of Washington, we found that students had a number of surprising difficulties learning about the photon and the photoelectric effect experiment. This research and how it led to the development of an interactive computer tutorial has been reported previously (Steinberg, Oberem, & McDermott, 1996; Ambrose et al., 1999). We summarize the results here.
Summary of Research
The research began with a study of student understanding
of physical optics, in which 46 college physics students were
interviewed on interference and diffraction (Ambrose et al., 1999).
In these interviews, students were asked about single-slit diffraction.
Sixteen of the students were in the introductory calculus-based
physics course, in which they had studied waves and optics. The
other 30 had completed this course and were taking modern physics.
All of the students were volunteers and almost all had above-average
grades in physics. The interviews, which were between 45 minutes
and one hour in length, were videotaped and analyzed. Surprisingly,
only 7 of the 46 students were able to explain the phenomena of
diffraction and answer simple questions about what would happen
to the pattern on the screen if the width of the slit were changed.
Furthermore, some unexpected beliefs about photons were expressed.
For example, some students described the photon as a point particle
traveling sinusoidally in space. It is worth noting that all of
the students were given as much time as they wanted to work through
the problem, and if they thought it were necessary, to correct
themselves as they went.
Student confusion with the concept of a photon led us to extend the scope of the interviews to include questions on the photoelectric experiment (Steinberg, Oberem, & McDermott, 1996). These interviews were conducted with six students from the modern physics class at the University of Washington. All six were doing well in the course and had completed their study of the photoelectric effect. The students were shown the schematic diagram of the experimental set-up from their text (Tipler, 1978). Fig. 1 contains a similar diagram. The students were asked to draw and interpret a graph of current versus voltage for a photoelectric experiment. If students were unable to draw an I-V graph, they were shown the one in their text and asked to account for its shape. The students were also asked about the effect on the graph of a change in intensity or frequency of the incident light. Throughout the interviews, students were asked to explain their reasoning. Some of the pronounced difficulties that we saw were:
· a belief that V = IR applies to
the photoelectric experiment
· an inability to differentiate between:
- intensity of light (and hence photon flux)
and
- frequency of light (and hence photon energy)
· a belief that a photon is a charged object
· an inability to make any prediction of an
I-V graph for the photoelectric experiment
. an inability to give any explanation relating photons
to the photoelectric effect
Subsequent research with many students taking the same
modern physics class revealed the widespread prevalence of these
difficulties. This suggests that many students lack a functional
understanding of the photon and the photoelectric effect.
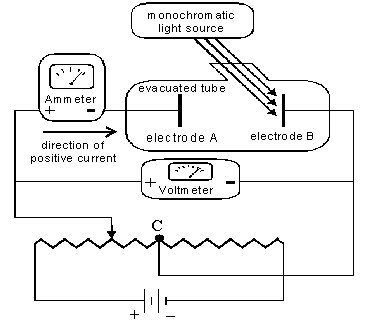 |
Figure 1: A schematic diagram of the photoelectric effect
apparatus. This diagram
is used in Photoelectric Tutor and is similar to the
one shown to students in our
interviews.
Development of Computer Tutorial
The University of Washington modern physics course does
not have an associated laboratory or discussion section. Furthermore,
the amount of time devoted to the topic is small. These constraints
suggested that a computer-based tutorial might be a practical
choice for developing supplementary instructional material on
the photoelectric effect. As we will show, computer technology
has allowed us to address student difficulties that we found in
our research and to engage students intellectually.
We decided to design a program, called Photoelectric Tutor, based on the simplified model of the photoelectric effect. Complicating factors that arise in a real experiment are typically not included in introductory courses and were not included in the program.2 Furthermore, the program assumes that the students have already been introduced to the photoelectric effect in the course they are taking. A strong case can be made to have students analyze a real experimental set-up and think critically about the results.3 However, we decided to focus on the more modest goal of helping students overcome some of the specific difficulties identified in our research. This decision was based on the severity of the difficulties that we found (post-instruction!) and the constraints of how the program was to be used. The basic features that we believe students should understand after having studied the photoelectric experiment are summarized below.
When light is incident on a metal, e.g. electorode B in Fig. 1, electrons are emitted if the photon energy hv is above a minimum value (the work function of the metal F). The maximum kinetic energy of the emitted electrons depends on the frequency of the light n, not on its intensity, and is equal to hv - F. If the frequency of the light is held fixed and hv > F, some of the electrons from electrode B reach electrode A, even when the potential difference V between the electrodes is zero. Thus there is a current even when V = 0. As V is made positive, electrons are attracted toward electrode A. The current therefore increases. For some positive value of V, essentially all of the emitted electrons reach electrode A and the current reaches a maximum value. When the voltage is made negative, electrons are repelled from electrode A. However, for small negative voltages, some electrons emitted from electrode B still have sufficient velocity to reach electrode A. As the voltage is made more negative, the number of electrons reaching electrode A decreases, and hence the current is less. Eventually, at some negative value for the voltage, called the stopping voltage Vs, virtually no electrons reach electrode A. At this voltage, eVs is equal to the maximum kinetic energy of the electrons. The current is essentially zero and remains so when the voltage is made more negative. The maximum kinetic energy of the emitted electrons does not depend on the intensity of the light. Hence, if the intensity of the incident light is increased, the stopping voltage will be unchanged. However, a greater number of electrons is emitted from electrode B and therefore at any given V > Vs the current is greater than in the case of light of lesser intensity. When there is no incident light, or when the frequency of the light is such that hv < F, the current is essentially zero.
Based on our interactions with modern physics students during and after our interviews, we believed that having students draw I-V graphs would be a good context for an instructional tool on the photoelectric effect. We decided to develop a computer program that would interpret student drawn graphs and infer difficulties the student had. The ability of the computer to interpret graphical input is therefore crucial. The program is written in cT, which is especially suitable for this purpose (Sherwood & Anderson, 1993).4
In order to keep the student engaged intellectually, the program enters into a dialogue with the student. The computer poses a sequence of questions, based on the studentís particular difficulty, and the student responds to each question by typing a short answer. The question sequence is determined by the studentís response to each question. In this way, students are led to confront and resolve their own difficulties.5 cT is specifically designed to facilitate the judging of short answers. It also readily supports the branching program structure needed to implement the question sequence used here.
Before using Photoelectric Tutor with a class,
we tested the program individually with five volunteers who had
previously taken the modern physics course. We asked the students
to think out loud as they worked through the program. This process
provided insights into difficulties that students were having
with the content or with the software. The information was critical
in refining the program before using it with a large numbers of
students. The program was then used during four successive quarters
in the modern physics class at the University of Washington (Steinberg,
Oberem, & McDermott, 1996). During this time, further research
was conducted into student understanding of the photoelectric
effect and the program continued to be
refined.
 |
Figure 2: Structure of Photoelectric Tutor. Students
have the option
to go to any part at any time (via the main menu), but the
program
suggests that they go through in a prescribed order.
OVERVIEW OF PROGRAM
Fig. 2 shows the structure of Photoelectric Tutor. All parts of the program are accessible from the main menu, which is the first screen that students see after the title page. If any part of the program is skipped, the computer will suggest that the student go back.
In the Introduction, students are shown a schematic for the circuit (Fig. 1) and provided with a description of the experimental setup. They are also given instructions on how to use the program. Students typically spend fewer than 5 minutes on this part and have little difficulty operating the program.
The main part of the program is broken into the parts described below. We describe how the computer is used to address difficulties that were revealed in our research.
Part I: Graphing I vs. V
Part I begins with a screen layout that includes a diagram
of the experiment, a set of axes on which I-V graphs can be drawn,
and a dialogue box in which the computer poses questions and students
type responses. (See Fig. 3.)
 |
Figure 3: Computer screen layout for Part I with a qualitatively
correct I-V graph.
The program looks for critical features of student drawn graphs,
interprets any
incorrect features, and gives students appropriate feedback.
Students are asked to use the mouse to draw a qualitatively correct graph of current versus voltage for the experiment as the voltage is varied from ñ5 Volts to +5 Volts. They do this by holding down the mouse button and dragging out a graph, or by clicking on a series of points to represent points on the graph. In the latter case, the computer automatically uses a straight line segment to join the points clicked. The computer constrains the graph to be single-valued and requires it to be drawn or clicked from left to right, i.e. from -5 volts to +5 volts. Students may start over at any time by clicking on the ìredraw graphî button. As a graph is drawn, the computer stores the points into a data array, performing a linear interpolation between points where necessary. Fig. 3 includes a qualitatively correct I-V graph which was drawn with a mouse.
When students finish drawing a graph, they click on the ìdoneî button. The program then analyzes the array of data corresponding to the graph drawn. The maximum current, the stopping voltage, and the voltage at which current saturation occurs are computed, if these features can be identified. In addition, the data are also searched for the presence or absence of certain qualitative features, some of which are indicative of student confusions. The features examined in the course of this analysis are embodied in the rules listed in Table 1. These rules are used by the program to check each graph. Although several qualitative features might be missing or incorrect in a single graph, the rules are hierarchical and thus a single rule will be selected to initiate a dialogue. The ordering of the rules is based on the order in which the underlying concepts should be learned and on the research summarized in the previous section. The program checks the rules against the input graph in the order in which they appear in Table 1.
Table 1: Heirarchical rules for checking qualitative features
of I-V graph. Photoelectric Tutor,
goes through these rules in order in determing what action
to take.
| Rules for qualitatively correct I-V graph |
Possible student confusion if rule is broken |
PhotoelectricTutor response if
rule is broken |
|
| 1 | graph must cover 90% of the voltage |
student has not drawn a complete graph |
asks student to redraw graph over wider voltage range |
| 2 | graph must not show a negative current for any voltage |
student fails to recognize that for a current to flow, electrons must be emitted from electrode B and flow towards electrode A |
dialogue on charge carriers being photoelectrons emitted from electrode B (see appendix) |
| 3 | graph must not pass through the origin |
student fails to recognize that some emitted electrons can reach electrode A even with V=0 |
dialogue on photoelectrons being emitted with a kinetic energy |
| 4 | current must level off at large positive voltages |
student fails to recognize that the charge carriers are limited to the emitted |
dialogue on the relationship between positive voltage and electric force on photoelectrons |
| 5 | current must be zero for large negative voltages |
student fails to represent the voltage at which electrons can no longer make it to electrode A |
dialogue on the relationship between negative voltage and electric force on photoelectrons |
| 6 | graph must not have negative slope anywhere |
student has not drawn a physically realistic I-V graph |
dialogue on the monotonic nature of the I-V graph |
| 7 | current must not saturate at a negative value of voltage |
student does not account for the fact that some electrons do not reach electrode A when there is no voltage |
dialogue on behavior within the vacuum tube when there is zero voltage (and hence zero electric field) |
A dialogue is associated with each of the rules. Each dialogue guides students to think about the concepts underlying the rule that has been broken by posing questions in an order that prompts a logical progression of thought. The dialogues take the form of branching sequences of questions. A student's track though a series of questions depends on the response to each question and can differ significantly from one student to the next. The dialogues are designed to make students recognize for themselves the logical inconsistencies in the incorrect graphs they draw.
Even after traditional instruction on the photoelectric effect, students did poorly in trying to draw a reasonable graph (Steinberg, Oberem, & McDermott, 1996). Only about 25% of modern physics students drew a qualitatively correct graph on the first try. The most common incorrect graph was a straight line drawn through the origin. This is consistent with performance in our interviews where students based their answers on Ohmís law. According to Table 1, the computer will trigger on rule 2 in this case. A sample dialogue that ensues is given in the appendix.
In all parts of the program, the computer keeps track of errors that have been made and concepts that have already been discussed. For example, suppose that a student draws a graph that does not show negative current and does include the current saturating for positive voltages but does not have the current zero for significant negative voltages. In this case, rule 5 of Table 1 will be matched. If the charge carriers in the tube and their source have not yet been discussed, the dialogue will begin with the same series of questions that would be used if rule 2 were broken. (See appendix.) If a rule is revisited because the error is still present in a graph, the student will simply be reminded of the conclusions previously agreed upon. A rudimentary student model consisting of a non-linked concept array is used to map the rules in Table 1 to the studentís interaction with the program. When a particular dialogue is initiated or reinitiated, the program examines this model to determine the style of interaction with the student and whether or not parts of other dialogues need to be incorporated, as explained above.
After each dialogue sequence, students are given the opportunity to redraw the graph. The process is repeated until a qualitatively correct graph is drawn.
Part II: Qualitative Problems
Part I of the program was designed to make sure that students
have a good qualitative understanding of the photoelectric effect
experiment. Part II of the program probes a little deeper to test
student understanding of the fundamental concepts involved. Students
are presented with a set of qualitative problems each of which
is designed to explore a particular concept fundamental to the
photoelectric effect. In each problem, students are shown a qualitatively
correct I-V graph and asked to sketch how the graph would
appear if a single change were made to the experiment. The screen
layout for this part of the program is shown in Fig. 4. The program
is designed to have students confront the types of difficulties
that we have seen in our research. Again the computer interprets
the student drawn graph and initiates an appropriate dialogue
with the student. Table 2 provides an overview of the four problems
used in Part II.
 |
Figure 4: Computer screen layout for Part II. In this part
of the program, students proceed
through the problems outlined in Table 2
Table 2: Overview of questions in Part II. For each problem,
students are shoen a qualitatively
correct I-V graph and asked to sketch how the graph
would appear if a single change were made.
The questions and ensuing dialogue are designed to address
conceptual difficulties we have seen.
| Description of qualitative question: |
Correct graph: | Common student drawn incorrect graph: |
Photoelectric Tutor response if graph orrectly |
| 1: light intensity is lowered |
current decreases but Vs stays the same |
lower Vs and lower
current- consistent with confusion be- tween effects of frequency and intensity |
dialogue contrasting the effect of increasing light intensity (photon flux) and light frequency (photon energy) |
| 2: light frequency is increased |
higher Vs | lower Vs - consistent with
failure to reason about the effect of a greater photon energy |
dialogue relating energy of photo- electrons, light frequency, and Vs |
| 3: metal with work function F>hv is |
current is zero for all voltages |
Vs on positive voltage axis
-in- dicative of failure to recognize conditions to get current to flow |
dialogue relating photon energy needed to emit electrons and the implications on current in the circuit |
| Challenge question: frequecy is exactly doubled |
stopping voltage is more than doubled |
incorrect Vs - indicative of failure
to apply photoelectric ideas in a more complex situation |
dialogue on the effect of increasing photon energy by a known amount |
Part III: Free Exploration
Part III allows students to explore the effect of varying
the experimental parameters on the I-V graph. The screen
layout of this part of the program is shown in Fig. 5. Students
are able to adjust the intensity of the light and the frequency
of the light. The frequency can be varied from 450 THz (670 nm)
to 1500 THz (200 nm). The intensity can be varied from zero to
some arbitrary maximum value corresponding to the maximum current
that will fit on the graph. In addition, five different metals
can be chosen for the electrode material. The work function of
each metal is purposely not revealed so that students can use
the program to figure out what each one is, for example, by adjusting
the frequency of the light until the current just becomes zero.
Parts I and II presume a photon model for light. In
Part III, students are given an opportunity to appreciate why
we believe the photon model of light is useful in describing our
observations. While this approach is in a sense backwards from
the process of science (where observations precede model development),
this is an approach that better matches the traditional instructional
setting. Furthermore, the importance of how observations lead
to the development of a photon model of light presumably was addressed
when students were first exposed to these ideas, which is typically
during lecture and reading.
 |
Figure 5: Computer screen layout for Part III. In this part
of the program, students can explore the
effects of varying the experimental parameters on the I-V
curve.
Electric Circuits Review
The original version of the program consisted of only the
three parts described above. However, when we first used the program
in a modern physics class, we saw that some students were having
difficulty understanding the electric circuit part of the schematic
diagram of Fig. 1. In the current version of the program, if student
answers during Parts I or II of the program indicate that they
are having problems with the circuit, the program recommends that
they go to the Electric Circuits Review. Students may also
work through this part of the program on their own choosing by
branching to it from the main menu page.
In this part of the program, the phototube in Fig. 1 is replaced by a fixed resistor and the rheostat is replaced by two fixed resistors connected in series to form a potential divider. As the sequence of questions progresses, the rheostat is eventually reintroduced as a variable potential divider.
MEASURING WHAT STUDENTS DO
An important part of our development strategy is continued feedback on student understanding of the subject matter and their interaction with the instruction. In this regard, Photoelectric Tutor can keep a complete record of its interaction with students. When data collection is enabled, the program records the data array corresponding to each graph students draw, including parameters such as the stopping potential associated with the graph. In addition, both sides of the dialogue are recorded. A second program, PhotoRead, is used to reconstruct the computer-student interaction. PhotoRead reproduces the graphs and presents the dialogues in the form of a transcript. These reconstructed interactions provide valuable insights into student thinking about the photoelectric effect and offer an opportunity to study the effect of the program on concept development for many students. We have used the results obtained in this way to help refine Photoelectric Tutor. The sample dialogue shown in the appendix was recovered using PhotoRead.
EVALUATION OF RESULTS
The photoelectric effect is commonly studied in classes that range from high school through graduate school. In this section, we detail implementations of Photoelectric Tutor in modern physics classes at the University of Washington and the University of Maryland.
University Modern Physics Class (Physics
Majors)
At the University of Washington, Photoelectric Tutor
was implemented as an optional homework assignment in 4 successive
quarters in a modern physics course. The course is considered
sophomore level and the majority of students are physics majors.
Based on the results of a series of examination questions related
to the photoelectric effect, students who went through the program
had a significantly better understanding of the relevant concepts
than the students who did not (Steinberg, Oberem, & McDermott,
1996). For example, we saw that weak students who used the program
outperformed stronger students who had not.
University Modern Physics Class (Engineering
Majors)
At the University of Maryland, a one-semester junior level
modern physics course is offered every semester. The majority
of the students in this course are engineering majors. The photoelectric
effect is a standard part of the instruction. Below, we contrast
student performance in successive implementations of this course.
Fall semester
During a recent Fall semester, there was traditional instruction
in the course and Photoelectric Tutor was not used. When
the instructor covered the photoelectric effect, he conducted
a standard lecture demonstration. He negatively charged a zinc
plate connected to an electroscope and the class observed the
leaf go up. He then shined an arc lamp on the plate and the class
observed the leaf go down. He also demonstrated the effect of
the arc lamp shined on the plate after it was charged positively.
(The electroscope leaf did not go down.) The fundamental principles
of the photoelectric effect were discussed. The instructor then
showed that a glass plate inserted between the arc lamp and a
negatively charged plate stops the electroscope from discharging.
The frequency dependence of the photoelectric effect was then
discussed in terms of the glass not transmitting the ultraviolet
light responsible for emitting the electrons. The standard photoelectric
experiment was also covered.
For the Fall semester, the class began with 22 students enrolled. By the first examination, only 10 students remained. The course was quite abstract and mathematically challenging and it appeared that the ones who continued were the stronger students.
Spring semester
During a recent Spring semester, the instructor had his
students use Photoelectric Tutor as the major part of his
classroom instruction on the photoelectric effect. The students
worked in groups of about three during one class session. The
program precipitated lively and productive discussion among the
students. It also created nice opportunities for the instructor
to recognize any difficulties that the students were having and
gave rise to instructor-student dialogues that were well matched
to the studentsí needs. However, since classroom time was
spent on the program, the instructor did not have an opportunity
to carry out the standard electroscope demonstration described
above.
For the Spring semester, the instructor was working on implementing an interactive and student-centered model of instruction. The drop rate was much lower than in the Fall semester. By the first examination, 18 students remained out of an initial enrollment of 23, including two students who took a make-up instead of the common examination described below.
Common examination question
In order to assess the success of using the program, an
identical question was administered on the first examination in
the Fall and Spring semesters. The question was directly related
to the demonstration done in the Fall and unrelated to the specific
context presented in Photoelectric Tutor. (See Fig. 6.)
It was nevertheless found that students in the Photoelectric
Tutor class did better than the students in the demonstration
class. (See Table 3.) This result is particularly impressive given
the high drop rate ñ of the apparently weaker students
ñ in the Fall semester compared to the Spring semester.
c) Would it be possible to discharge the electroscope
by replacing the metal plate with a plate made d) Would the electroscope discharge of the same
experiment as above were repeated except with the |
Figure 6: Examination question on the photoelectric effect.
The question was administered to
two university modern physics classes mostly of junior engineering
students.
Parts A and B of the examination question address changes in the photon flux and photon energy. Part C addresses the concept of work function. In each of these parts, the Photoelectric Tutor class scored better than the demonstration class. It is encouraging that the students who worked through the program appear to be able to apply their conceptual understanding in a very different context from that in which they learned it.
Part D asked whether it is possible to discharge a positively charged plate via the photoelectric effect. Since only electrons are emitted by photons, the correct answer is clearly no. This was part of the demonstration shown in the Fall semester. However, half of the students in the demonstration class did not answer this correctly. Students who got this wrong apparently did not have a physical model for the photoelectric effect. For example, one student wrote ìwhen light interacts with matter like above experiment (sic) there will be photoelectric effect regardless of the type of charged particles.î In contrast, in the Photoelectric Tutor class, more than 80% of the class answered correctly, even though they had not seen the demonstration.
Table 3: Percentage of students giving correct response
to exam question shown in Fig.6. In the
electroscope demo class, students were shown a demondtration
similar to the one described in
the exam question. In the Photoelectric Tutor class,
students did not see the demo and instead
went through the computer program. Note that the higher drop
rate in the demondtration class
(55% vs. 22%) resulted in selective dropping of the weaker
students.
| Correct response |
Percentage correct: Class with electroscope demo (N = 10) |
Percentage correct: Class using Photoelectric utor (N = 16) |
|
| possible to discharge by incresing intensity? |
no | 70% | 81% |
| possible to discharge by increasing frequency? |
yes | 60% | 81% |
| possible to discharge by changing metal? |
yes | 70% | 88% |
| possible to discharge if metal were charged posi- tively |
no | 50% | 81% |
OTHER EXAMPLES
At the University of Maryland, we are developing a new modern physics / quantum mechanics course that is intended to be accessible to a wide audience. (See note 1.) Two key features of the course are the use of physics education research and instructional technology. In this paper we have detailed how we have combined these two elements in the instruction of the photoelectric effect. As another example, we have identified and addressed student difficulties with potential energy diagrams, which are crucial to learning about band diagrams and quantum wells. Our research has shown that students lack an understanding of the classical relationship between force and potential energy, that they have confusions with energy graphs, and that they are subsequently unable to interpret representations of energies and probabilities in quantum systems. In response, we have developed classroom activities that address these difficulties. In one activity, students use a force probe interfaced with a computer to observe graphs of force vs. motion and then to reason about graphs of potential energy vs. motion.6 Students work towards interpreting potential energy diagrams and probability curves in quantum systems.
We have used the force probe lesson, as well as others in the classroom (e.g. Bao, Redish, & Steinberg, 1998). Students are engaged and the level of difficulty seems appropriate. While working through the activities, many students confront the difficulties our research has indicated are widely prevalent. Furthermore, student performance on examinations suggest that the lessons are useful in improving student understanding of the subject matter.
CONCLUSIONS
In this paper, we have described the development of new
instructional materials in modern physics. We have shown how we
used physics education research and computer technology to design,
evaluate, and refine the materials. Our overall approach to instructional
reform is diagrammed in Fig. 7. Our results suggest that this
approach is effective in helping many students learn difficult
topics in physics. While we have focused on one specific context
in this paper, the approach depicted in Fig. 7 has general utility
in the development of technological teaching tools.
 |
Figure 7: Schematic for our development of intructional
materials. We try to develop all
of our materials (both computer-based and not) with a founction
in research into student
understanding, with a style that engages the student intellectually,
and with a great care
put into the testing of the materials in real classes settings.
References
Ambrose, B.S., Shaffer, P.S., Steinberg, R.N., and McDermott,
L.C. (1999). An investigation of student understanding of single-slit
diffraction and double-slit interference. American Journal
of Physics 67, 146-155.
Arons, A.B. (1990). A Guide to Introductory Physics Teaching. New York: John Wiley & Sons, Inc., New York, 245-250.
Grayson, D.J. (1996). Using education research to develop waves
courseware. Computers in Physics, 10(1), 30-XXX.
Jolly, P., Zollman, D., Rebello, N.S., and Dimitrova, A. (1998).
Visualizing motion in potential wells. American Journal of
Physics, 66, 57-63.
Laws, P.W. (1997). Promoting active learning based on physics education research in introductory physics courses. American Journal of Physics,65, 13-21.
Bao, L., Redish, E.F., and Steinberg, R.N. (1998). Student misunderstandings of the quantum wavefunction. AAPT Announcer, 28(2), 92.
McDermott, L.C. and Redish, E.F. (1999). Resource Letter on Physics Education Research. to appear in American Journal of Physics.
McDermott, L.C. (1991). What we teach and what is learned - Closing the gap. American Journal of Physics, 59, 301-315.
Oberem, G.E. and Steinberg, R.N. (1999). Photoelectric Tutor. College Park, MD: Physics Academic Software, American Institute of Physics.
Preston. D.W., and Dietz, E.R. (1991). The Art of Experimental Physics. 166-180.
Redish, E.F. and Steinberg, R.N. (1999). Teaching physics: Figuring out what works. Physics Today, 52(1), 24-30.
Sherwood, B.A. and Andersen, D.M. (1993). cT creates prize-winning portable physics programs,î Computers in Physics, 7(2), 136-143.
Steinberg, R.N., Oberem, G.E., and McDermott, L.C. (1996). Development of a computer-based tutorial on the photoelectric effect. American Journal of Physics, 64, 1370-1379.
Thornton, R.K., and Sokoloff, D.R. (1990). Learning motion concepts using real-time micro-computer based learning tools. American Journal of Physics, 58, 858-870.
Tipler, P.A. (1978). Modern Physics. New York: Worth Publishers, 107.
Appendix: Sample Computer Student Dialogue
A sample dialogue between computer (C) and student (S)
that occurs after the student draws an I-V graph which
includes a negative value for current.
C: Ok. Letís discuss the graph you have
drawn.
When there is a current flowing
in the circuit, what are the charge carriers.
S: electrons
C: Ok! Electrons are the charge carriers.
When there is a reading on the ammeter,
is there a flow of electrons in the space between the electrodes?
S: Yes
C: Ok! There must be a flow of charge everywhere in
the circuit.
If there is a flow of electrons
in the vacuum tube, they must be ejected from an electrode.
What makes
these electrons be ejected from
the electrode?
S: the voltage between the electrodes
C: Do you think 5 volts between two pieces of metal separated
by several inches would be enough to remove
electrons from either piece of
metal?
S: no
C: I agree. You would need a much larger voltage.
So, what makes these electrons
be ejected?
S: the light incident on the electrode
C: Good! Light (photons) striking an electrode can
cause electrons to be ejected.
Would you expect electrons to be
ejected into the vacuum from: a) only electrode A, b) only
electrode B,
or c) both electrodes? (Type a,
b, or c.)
S: c
C: We agreed that light is needed for electrons to be ejected
into the vacuum. No light is incident on electrode
A.
So, from where are the electrons
being ejected
S: b
C: Right! Electrons are ejected into the vacuum only
from electrode B because no light strikes electrode A.
If electrons are being ejected
into the vacuum only from electrode B, will conventional current
flow a) only
from left to right through
the ammeter, or b) only from right to left through the ammeter,
or c) both?
S: a
C: Right. Since electrons only go from electrode B
to electrode A, conventional current will only flow from left
to right through the ammeter.
If the conventional current flows
only from left to right in the ammeter, will the ammeter read
negative at any
time?
S: no
C: Good! The ammeter will not read negative in this
experiment.
Your graph shows negative values of current.
You should redraw your graph to be consistent
with the idea that the current will only be positive.
This work has been funded in part by the National Science Foundation, the Fund for the Improvement of Postsecondary Education, and California State University, San Marcos.
Author Note
We would like to thank members of the Physics Education
Groups at the Universities of Washington and Maryland for their
many contributions to the work described in this paper. We would
also like to thank the participating modern physics course instructors
for their generous cooperation during the development and testing
of new materials.
Notes
1. E.F. Redish and R.N. Steinberg, A New Model
Course in Quantum Mechanics for Scientists and
Engineers, National Science Foundation,
DUE 9652877; E.F. Redish and R.N. Steinberg, Practical
Quantum Mechanics: Opening a door for tomorrow's
engineers, inventors, and scientists, Department
of Education FIPSE grant 116B70186.
2. These factors include the effects of the
contact potential between electrodes of different metals, thermionic
emission of electrons from the electrodes,
and reverse current. For example, see Preston and Dietz
(1991).
3. For an example that is described in detail,
see Arons, (1990). Students are guided through the sequence
of inductive reasoning that leads from Lenardís
experimental observations to invention of the photon model.
4. cT is distributed by Physics Academic Software, American Institute of Physics, College Park, MD.
5. For an overview of the elicit / confront
/ resolve instructional strategy used by the University of Washington
Physics Education Group, see McDermott (1991).
6. This activity is based on one described
in Jolly et al. (1998).