1) A boy and a girl are tossing an apple back and forth between them.
The sketch at the right shows the path the apple followed when watched
by an observer looking on from the side. The apple is moving from the left
to the right. Five points are marked on the path. Ignore air resistance.
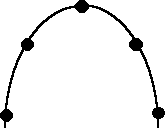
(a) Make a copy of this figure. At each of the marked points, draw an
arrow that indicates the magnitude and direction of the apple's velocity
when it passes through that point.
(b) Make a second copy of the figure. This time, at each marked point,
place an arrow indicating the magnitude and direction of any force the
apple feels at the instant it passes that point.
2) Student A says: Galileo said all objects fall with the same speed.
I know that's not true. If I drop a balloon and a billiard ball the balloon
falls more slowly. Galileo was wrong.
Student B says: No. Galileo only said two heavy objects fall with the
same speed. If I drop a steel ball and a wooden ball they hit the ground
at the same time.
Discuss these student's statements. Which one do you agree with? If
either or both are wrong, explain why.
3) Consider a metal sphere two inches in diameter (S) and a feather
(F). For each quantity in the list below indicate the relation between
the quantity for S and F. Is it the same, greater, or lesser? Explain in
each case why you gave the answer you did.
- (a) The gravitational force
- (b) The time it will take to fall a given distance in air
- (c) The time it will take to fall a given distance in vacuum
- (d) The total force on the object when falling in vacuum
- (e) The total force on the object when falling in air.
4) In C. S. Forster's novel Lieutenant Hornblower (set in the early
1800's) a British naval vessel tries to sneak by a Spanish garrison. The
ship passes as far away from the Spanish guns as it can -- a distance s.
The Spanish gunner knows that his gun has a muzzle velocity equal to v0.

(a) Once the gun is fired, what controls the motion of the cannonball?
Write the equations that determine the vector acceleration of the cannonball
after it leaves the cannon. You may ignore air resistance.
(b) Suppose the gunner inclines his gun upward an angle q to the horizontal.
Solve the equations you have written in (a) to obtain expressions which
can be evaluated to give the position of the cannonball at any time, t.
(c) If the gunner wants the cannonball to hit the ship, he must choose
his angle correctly. Explain how he can calculate the correct angle. (Again,
you may ignore air resistance.)
(d) If the muzzle velocity of the cannon is 100 m/s and the ship is a distance
of 1/2 a kilometer away, find the angle the gunner should use. (Take g
to be 10 m/s/s.)
You may need one of the following trigonometric identities (true for
all angles theta):
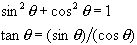
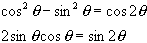
5) A golfer is trying to hit a golf ball onto the green. The green is
a horizontal distance s from his tee and it is up on the side of a hill
a height h above his tee. When he strikes the ball it leaves the tee at
an angle theta to the horizontal. He wants to know with what speed, v0,
the ball must leave the tee in order to reach the height h at the distance
s.
(a) Once he has struck the ball, what controls its motion? Write the
equations that determine the vector acceleration of the golf ball after
it leaves the tee. Be sure to specify your coordinate system. For this
part of the problem you may ignore air resistance.
(b) Solve the equations you have written in (a) to obtain expressions which
can be evaluated to give the position of the ball at any time, t.
(c) If the golfer wants his ball to land in the right place, he must hit
it so that it leaves the tee with the right speed. Explain how he can calculate
it. (Again, you may ignore air resistance.) Find an equation for the initial
speed in terms of the problem's givens.
(d) If the ball leaves the tee at an angle of 30º, s is 100 m, and
h is 10 m, find the speed with which the ball should leave the tee.
(e) Now consider the effect of air resistance. Suppose that a good model
for the force of air resistance is the Newton drag law,
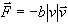
where |v| stands for the absolute value of the velocity -- the speed. consider
three points of the ball's trajectory -- halfway up, at its highest point,
and halfway down. Discuss the direction of the resistance force at each
place. Qualitatively (do not attempt a calculation!), what will the effect
of air resistance be on the ball's motion?
6) The Baltimore Orioles are playing the Boston Red Sox at Fenway Park
in Boston. Cal Ripken hits a long fly ball. The ball left his bat at a
speed V at an angle of theta above the horizontal. The ball heads towards
the "Green monster" in left field -- a high fence. The fence
is a distance s from Ripken at home plate and its height is h.
(a) Draw a labeled diagram of what is happening.
(b) Make some reasonable approximations to simplify the problem. State
them clearly. Then, write and solve the equations of motion for the motion
of the ball.
(c) Derive an equation that will tell you what the ball's height will be
when it reaches the fence.
(d) For the particular case involved, V = 120 ft/s, theta = 45º, s
= 360 ft, and h = 100 ft. Will the ball go over the fence?
7) A test rocket containing a probe to determine the composition of
the upper atmosphere is fired vertically upward from an initial position
at ground level. During the time T while its fuel supply lasts, it ascends
with a constant upward acceleration of magnitude 2g. Assume that air resistance
can be neglected and that the rocket goes a small enough height that the
earth's gravitational force can be assumed to be constant.
(a) What is the speed and height of the rocket above ground level when
the fuel runs out?
(b) What is the total height the rocket will reach above the ground?
(c) If T is 30 seconds, how high will the rocket get?
| 8) A heavy projectile is thrown and follows a path something like the
one shown in the figure at the right. For each of the quantities in the
list (a) - (d) below, select a direction from one of the choices in the
list A - G. If you think that none of the choices apply, put an N. |
 |
| Quantities: |
Choices: |
| a) The projectile's velocity when it is at the highest point. |
A. Points straight up. |
| (b) The force on the projectile when it is part way up. |
B. Points straight down. |
| (c) The force on the projectile when it is at the highest point. |
C. Points directly to the left. |
| (d) The projectile's acceleration when it is part way down. |
D. Points directly to the right. |
|
E. Is equal to zero. |
|
F. Points somewhat upward and to the right. |
|
G. Points somewhat upward and to the left. |
|
N. None of the above. |
9) In our readings about mechanics we encounter the following equations:
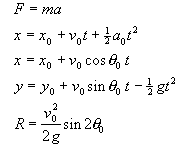
For each equation, discuss the following questions.
- What is the physical system being described by this equation?
- What does each symbol represent?
- Under what conditions does the equation hold?
Sketch on your paper a diagram in which you put each of the equations
in a box. Connect with an arrow any pair of equations when one equation
can be easily derived from another by considering a special case. (The
arrow should point from the more general to the more specific equation.)




![]()
![]()
![]()

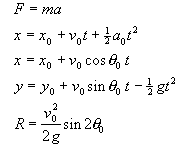
![]()