
Problems for
Intermediate Methods in Theoretical PhysicsEdward F. Redish
 |
|
| A small cart of mass m with (nearly) frictionless wheels is connected to a spring of spring constant k. It is connected to a plunger imbedded in light oil as shown in the figure at the right. The oil provides a damping force of -bv. |
 |
The cart is struck at time t = 0 by a quick tap with a hammer. We'll model this system by the equation of motion
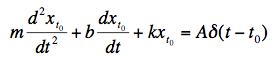
(a) What are the dimensions of the constant A?
(b) Assuming that the cart is initially at x = 0 and is at rest, use the Fourier transform to solve for xt0(t),the position of the cart as a function of time when it is struck at a time t0.
(c) Show that for a general function, f(t), we can write
 .
.
Show why this works, starting from the equation given above part (a). (You don't have to show that the solutions agree.)
Last revision 12. December, 2005.