
Problems for
Intermediate Methods in Theoretical PhysicsEdward F. Redish
 |
|
| Consider two masses connected to each other and to two rigid walls by three identical springs. We make the following approximations:
|
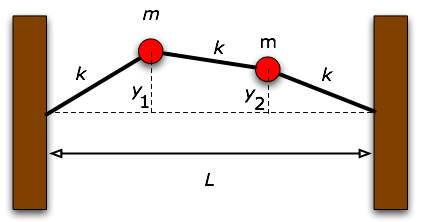 |
(a) For an arbitrary pair of displacements y1 and y2 find the net forces acting on each of the masses and write Newton's second law for each mass.
(b) Assume both displacements remain very small compared to L so that terms of the the order of (y/L)2 can be ignored compared to first order terms. Show that the equations of motion reduce to equations very similar to the ones we derived for longitudinally moving masses but with an effective k. Express keffective in terms of the parameters of the problem: T, m, l0, and L.
(c) Without solving the problem mathematically, describe what you think the normal modes will look like and what their frequencies might be.
Last revision 7. November, 2005.