
Problems for
Intermediate Methods in Theoretical PhysicsEdward F. Redish
 |
|
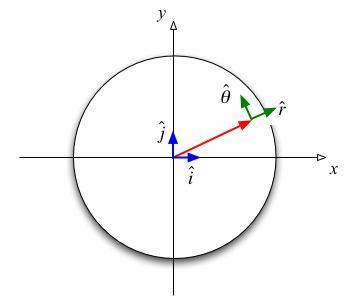
| Consider the matter in a uniform disk rotating about its symmetry axis. Using the polar version of the coordinate system shown in the figure at the right, this can be written as
Note we are here using cylindrical polar coordinates and referring to the cylindrical radius,
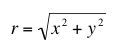 . .We can define a vector field, that specifies what velocity would be for the matter found at the point (x,y,z) at the time t. The disk has radius R and the base of the wheel is located in the z=0 plane and the wheel has a thickness d. |
 |
(a) If the wheel is rotating at a uniform angular velocity ω0 specify the velocity field at all points in space by explicitly writing its x, y, and z components as a function of the x, y, z, and t space and time coordinates.
(b) Explicitly write the components of the velocity of the bit of matter at the point (x,0,0) (x<R ) as a function of time.
(c) Compare and contrast your two velocity functions. Pay particular note to
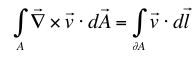 ,
,showing explicitly the vector components of every vector involved and working out all dot and cross products. Do not skip steps and be sure to state what you are doing in each step.
Last revision 5. December, 2004.