
Problems for
Intermediate Methods in Theoretical PhysicsEdward F. Redish
 |
|
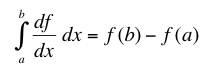 .
.When we do this in vector form, the results are more complicated. If we have a scalar field, f, and a vector field, F, then we typically consider three theorems in three dimensions where an integral cancels a vector derivative:
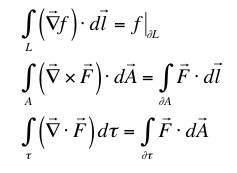 .
.[We have used the mathematical notation "∂" to represent the boundary of a region in space. The boundary of an open line is its two endpoints, of an open area is the loop surrounding it, and of a volume is the surface covering it. Note that the boundary of a closed region -- a loop, or a sphere, for example -- is 0. This convenient notation is used in manifold theory.]
In each of these, a derivative (here in vector form) cancels one integral -- in the latter two cases still leaving some integrations. (The first doesn't really have a name but you can think of it as "the potential theorem." It says that the line integral of a vector field that is the gradient of a potential is the difference of the potential at the end points. The second is Stoke's theorem and the third is basically Gauss's theorem.)
If we have a scalar function f and a vector function F, we can take vector derivatives of them to create three quantitites.
(There is actually a fourth we can create: a second-rank tensor, but we will not consider this here and these can be shown to exhaust the possibilities.)
Now we can consider integrating each of these over a line, L, over an area, A, and over a volume, τ. The small bit of a line and of an area we add up are vectors while the small bit of a volume is a scalar. We could combine our scalar (the divergence) with these three in only one way and we could combine our vectors (the gradient and the curl) with the volume in only one way. But we could combine our vectors (gradient and curl) with the vectors of length and area in two ways: as dot or cross products.
From the combinations described above, we could put together 13 integrals of derivatives and therefore could in principle have 13 different forms of the fundamental theorem of calculus. We have only talked about three. Of the other 10, some are correct, others are not. Consider the following two possible forms of an integral of a vector derivative and decide whether you can have the derivative cancel one of the integrals. That is, are either of these expressions equal to something with no derivative and one less integral? If it is, give it. If it isn't, explain why not. (Hint: Consider the integral of the derivative over a small, conveniently oriented surface or line.)
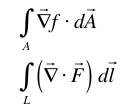 .
.Starting with these two examples, give a plausible heuristic of how we might be able to tell (without proof) whether the other 8 possibilities worked or didn't.
Last revision 28. December, 2010.