Problems for
Intermediate Methods in Theoretical Physics

Edward F. Redish

The Gibbs Phenomenon

When we try to use a Fourier series (or any expansion) that doesn't match the character of the basis (normal modes) we are using to expand it, funny things sometimes happen. A reasonably straightforward example of this is what happens when we try to expand a square wave (that's not really continuous and definitely doesn't have a well defined derivative) in an ordinary Fourier series. Let's try it.

(a) Consider trying to shape a string tied down at both ends (y(0,t) = y(L,t) = 0) into a square wave:

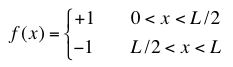
Note we can't really define this function at the joining points since it's not really continuous. We can imagine the rises and falls are sharp, but not infinitely fast.

Expand this function in a Fourier series in the normal modes of the string tied down at both ends by calculating the coefficients fn:

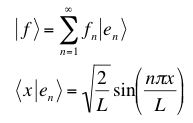
(Hint: Use Dirac notation and the Parity operator to eliminate unneccessary calculations.)

(b) Use a numeric calculation (either Mathematica or a spreadsheet) to calculate and plot the partial sums of the series for the first 6 non-zero terms.

(c) By looking at the shape of f and of the Fourier terms, give a qualitative argument (from symmetry) explaining why the terms that vanish cannot contribute.

(d) The "wiggling ears" that you should find at the edges of the Fourier sums do not go away as you add more and more terms. They settle down in size, but get "squeezed" more and more towards the beginning and end of the 0-L region. This is called the Gibbs phenomenon. What that means is that the partial sums

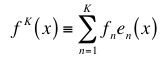
converge in an integrated sense but not in a point-by-point sense; that is:

.

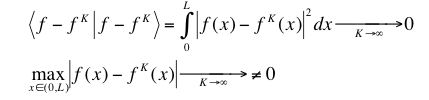Explain how this can happen in terms of what the functions f K(x) are doing and get an estimate for what the maximum value of |f(x) - f K(x)| for all x is as K → ∞.

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 13. November, 2005.