Problems for
Intermediate Methods in Theoretical Physics

Edward F. Redish

Solving the Wave Equation

Consider the wave equation for the transverse displacement of a taut elastic string. The equation for the displacement, y, of a bit of string at the point x at time t, y(x,t) is usually written

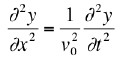
(a) Change the variables in the equation from x, t to ξ, η ("xi" and "eta") where

ξ = x - v0t
η = x + v0t

(b) Show that any arbitrary pair of functions (as long as they have two well-defined derivatives) f and g lead to a solution of the wave equation

y(ξ, η) = f(ξ) + g(η)

(c) Rewrite y of the solution in part (b) as a function of x and t. Interpret f and g physically, explaining why you interpet them as you do.

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 7. November, 2005.