
Problems for
Intermediate Methods in Theoretical PhysicsEdward F. Redish
 |
|
Last week we considered the set of functions consisting of the sum of the two functions sin θ and cos θ:
where a and b are arbitrary complex numbers. We can associate this function with a vector
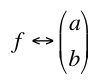
and we proved that this set of functions forms a linear space.
(a) From the usual definition of inner product in our vector space describing the motion of a single particle in one dimension, we might come up with one or more definitions of an inner product in this space. Construct one and show that it doesn't work -- that it doesn't give an inner product according to the definition given in class on Monday. Discuss why this is the case.
(b) Show that the definition
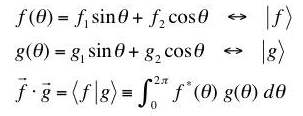
satisfies the conditions for an inner product.
(c) What is the dimension, n, of the inner product space constructed in parts (a) and (c)? Construct a set of n orthonormal vectors in this space that can serve as a basis.
Last revision 28. October, 2004.