Problems for Intermediate Methods in Theoretical Physics Edward F. Redish

When studying the orbits of an object of mass m around a planet of mass M it is useful to create an “effective radial potential” that is only a function of the raidus and has the form

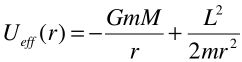
where L is the object’s orbital angular momentum. With a little algebra and dimensional analysis (don’t do it now) we can write this in the more convenient form

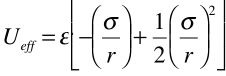
(a) Sketch what the curve of U_eff(r) looks like as a function of r identifying the salient points (maxima or minima, crossings of 0) by giving an expression for them in terms of the constants σ and ε.

(b) Expand U_eff(r) in a power series about the location of its minimum value, r₀, to second order. Sketch the same figure you drew in (a) but this time add onto it a sketch of the second order power series approximation you have generated.

(c) Identify the “effective spring constant”, k, that would give an approximation for U_eff(r) in the neighborhood of its minimum,

.

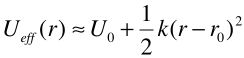Last revision 27. December, 2010