
Problems for
Intermediate Methods in Theoretical PhysicsEdward F. Redish
 |
|
| Consider a simple harmonic oscillator (e.g., an idealized cart connected to a massless spring as shown in the figure at the right). In this problem, you will solve the equation of motion numerically as weel as analytically and explore the accuracy of your results. Assume the cart has a mass m and the spring has a spring constant k. For this problem, do not convert to dimensionless quantities. | 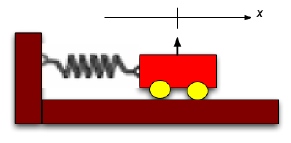 |
Last revision 14. September, 2004.