Homework 1

1-1

Generally a simple harmonic oscillation can be expressed as $f(t) = C_1 \cos \omega t + C_2 \sin \omega t$, and the coefficients $C_1, ~C_2$ are determined by the initial condition (at $t=0$, for instance). (a) By taking $f(0)=x_i$ and $f^\prime(0)= v_i$, you can show that $C_1 = x_i$ and $C_2 = v_i/\omega$. (b) Just an algebraic (trigonometric) identity.

1-2

The wave motion is $y = A~\sin( \omega t +\alpha)$, the speed is $dy/dt = \omega A~\cos (\omega t +\alpha )$, the acceleration $d^2y/dt^2 =-\omega ^2 A~\sin(\omega t +\alpha )$. Here $\omega = 2\pi \times 2000 ~\rm Hz \approx 1.25 \times 10^4 ~\rm s^{-1}$, $A = 0.40 ~\rm mm$. (a) The maximum acceleration = $\omega^2 A \approx 6.3 \times 10^4 ~\rm m/s^2$, and the max speed $\omega A \approx 2.5~\rm m/s$. (b) When $y(t)=d= 0.02~\rm mm$, the acceleration= $y^{\prime\prime} (t)=\omega ^2 d\approx 3.2 \times 10^3 ~\rm m/s^2$, and the speed= $y^\prime (t) = \omega \sqrt{ A^2-d^2}\approx 2.5 ~\rm m/s$ from the identity $\sin^2(x)+\cos^2(x) =1$.

1-3

This is a real-life example of a mass-spring system. (a) The total mass at the end of the spring is $M+m$, and so the relationship between the period $T$, spring constant $k$, and the total mass is

$$M+m = kT^2/(4\pi ^2)~.$$

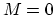
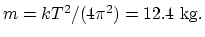
(b) In this case, $M=0$, so $m = kT^2/(4\pi ^2)= 12.4 ~\rm kg.$ (c) $M = kT^2/(4\pi ^2)-m = 54.0~\rm kg.$

1-4

$f= 3.0 ~\rm Hz$. (a) $M = 1450 ~\rm kg$. Then $k = 4\pi^2 M f^2 = 5.15\times 10^5 ~\rm kg/s^2$. (b) An additional mass $m=5\times 73 ~\rm kg$ is added to the system. The result is $f= \sqrt{ k\over 4\pi ^2 (M+m)} = 2.68 ~\rm Hz$.

1-5

(a) For S.H.O., $a(t)=-\omega ^2 x(t)$. So $f= \sqrt{-a/x}/2\pi =5.58 ~\rm Hz$. (b) $m =k/(4\pi^2 f^2)= 0.325 ~\rm kg$. (c) From the relation $v^2 -ax = \omega^2 A^2$, $A= \sqrt{v^2-ax}/\omega =0.4 ~\rm m$.

1-6

Given info: $E = {m\over 2}\omega ^2 A^2 = 1.0~\rm J$, $A= 0.10 ~\rm m$, and $v_{\rm max} = \omega A = 1.2 ~\rm m/s$. Firstly, the frequency is just $\omega/2\pi= f = v_{\rm max}/(2\pi A) =1.9 ~\rm Hz$. Secondly, from the known energy and the frequency, $m = {2E\over \omega ^2 A^2}=1.4 ~\rm kg$. Lastly, $k = 4\pi ^2 m f^2 = 200 ~\rm N/m$.

1-7

$m=2.0 ~\rm kg$ and $A=0.200 ~\rm m$. (a) $k = F/x = 100 ~\rm N/m$. (b) $f = {1\over 2\pi} \sqrt{k/m} = 1.13~\rm Hz = \omega /2\pi$. (c) $v_{\rm max} = \omega A = 1.42 ~\rm m/s$. (d) $a_{\rm max} = \omega ^2 A =10.1 ~\rm m/s^2$. (e) $E= {1\over 2}m\omega ^2 A^2 =2.02 ~\rm J$. Now if $x(t_0) = A/3$ at certain $t=t_0$, (g) $a(t_0) = -\omega ^2 x(t_0)=3.36 ~\rm m/s^2$. (f) $v(t_0)= \omega \sqrt{A^2 - x^2(t_0)} = 1.34 ~\rm m/s$.

1-8

This is a physical pendulum with a moment of inertia $I= {1\over 12}mL^2 +md^2$ (note: parallel axis theorem) with a gravitational force (torque) action at a distance $d$. Then the small amplitude period of oscillation is $T = 2\pi \sqrt{ {1\over 12}mL^2 +md^2\over mgh}$.

1-9

You first have to understand that the constant $g$ in the formula $T= 2\pi \sqrt{L/g}$ is actually the total effective acceleration on the mass $m$. Inside a frame with an upward acceleration $a$, the total effective acceleration is $g^\prime = g +a$. (a) $g^\prime = 14.8 ~\rm m/s^2$and $T= 3.65 ~\rm s$. (b) $g^\prime = 4.8 ~\rm m/s^2$, and $T= =6.41 ~\rm s$ (c) The effective acceleration is obtained by vector addition $g^\prime = \sqrt{ g^2+ a^2}= 11~\rm m/s^2$, and $T= 4.24 ~\rm s$.

1-10

$m=12.5~\rm kg$ and $k=4.30 ~\rm kN/m$. (a) The natural frequency of the system is ${1\over 2\pi}\sqrt{k/m} = 2.95 ~\rm Hz$. (b) The physical contact between the mass and the spring is minimal (zero) when the downward acceleration is equal to the gravitation. $A = mg/k = 2.85 ~\rm cm$.