| Name: |
|---|
Physics 161
7/13/2001
There are 6 questions worth 20 points each with point breakdowns listed in square brackets. Show ALL your work. If you need more workspace, use the back of the same page and write a note indicating this.
1. A few questions
(a) [6 pts] Describe what is meant by an inertial and a non-inertial reference frame. Compare the two in terms of how an observer in each might apply Newton's laws.
(b) [6 pts] How are linear and angular momentum related? When is linear momentum conserved? When is angular momentum conserved?
(c) [8 pts] An astronaut on a research mission to asteroid 1566, named Icarus, ponders whether she can escape the asteroid's gravitational pull simply by jumping upwards from the surface. Icarus has a diameter of ![]() km and a mass of
km and a mass of ![]() kg and the universal gravitational constant
kg and the universal gravitational constant
![]() N
N![]() m
m![]() /kg
/kg![]() . Calculate the escape speed of Icarus and comment whether a person might achieve this speed by jumping.
. Calculate the escape speed of Icarus and comment whether a person might achieve this speed by jumping.
2. A puck of mass ![]() kg initially at rest on a horizontal, frictionless surface, is struck by a second puck of mass
kg initially at rest on a horizontal, frictionless surface, is struck by a second puck of mass ![]() kg. The second puck is moving initially with speed
kg. The second puck is moving initially with speed ![]() m/s in the positive
m/s in the positive ![]() direction and after the collision moves with a speed
direction and after the collision moves with a speed ![]() m/s at an angle
m/s at an angle
![]() from the positive
from the positive ![]() axis.
axis.
(a) [8 pts] Determine the velocity of the first puck ![]() after the collision.
after the collision.
(b) [7 pts] Find the fraction of kinetic energy lost in the collision (![]() ). Where does this energy go?
). Where does this energy go?
(c) [5 pts] What is the impulse delivered to puck ![]() ?
?
3. The velocity versus time graph for an object traveling along a straight line is given below. The initial position of the object at ![]() s is
s is ![]() m.
m.
(a) [7 pts] Graph the acceleration versus time on the bottom graph.
Include numeric values on the acceleration axis (ordinate axis) to indicate the scale.
(b) [7 pts] Graph the position versus time on the top graph. Include
numeric values on the position axis (ordinate axis) to indicate the scale.
(c) [6 pts] What is the value of the position at ![]() and 25 seconds?
and 25 seconds?
![\includegraphics [clip]{fig_xvat2.eps}](img17.gif)
4. Several constant forces are applied to a wheel as shown. Note ![]() is applied at an angle
is applied at an angle
![]() relative to the tangent. The values of the radii are given by
relative to the tangent. The values of the radii are given by ![]() cm and
cm and ![]() cm. The wheel has a mass
cm. The wheel has a mass ![]() kg and can be considered to be a uniform disk of radius
kg and can be considered to be a uniform disk of radius ![]() .
.
![\includegraphics [clip]{fig4.eps}](img24.gif)
(a) [5 pts] Find the net torque acting on the wheel. Reminder: torque is a vector.
(b) [5 pts] If the torque in part (a) acts continuously on the wheel, which is initially at rest, find the angular speed after 3.0 seconds.
(c) [5 pts] How many revolutions does the wheel make during this time?
(d) [5 pts] What is the net work done on the wheel?
5. A wad of putty with mass ![]() travels with initial speed
travels with initial speed ![]() . The putty
hits and sticks to the end of a uniform rod of length
. The putty
hits and sticks to the end of a uniform rod of length ![]() and mass
and mass ![]() . The rod is free to rotate in a horizontal plane about a fixed vertical axis through its center of mass. Where appropriate, express your answers in terms of
. The rod is free to rotate in a horizontal plane about a fixed vertical axis through its center of mass. Where appropriate, express your answers in terms of ![]() and
and ![]() .
.
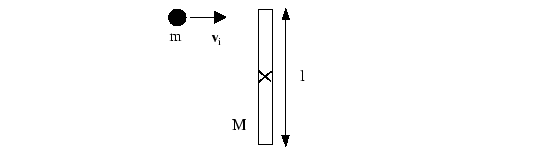
(a) [3 pts] Find the initial angular momentum ![]() of the putty about the axis of the rod. Be sure to specify magnitude and direction.
of the putty about the axis of the rod. Be sure to specify magnitude and direction.
(b) [5 pts] Calculate the moment of inertia of the putty and rod about the axis of the rod.
(c) [6 pts] What is the final angular velocity ![]() of the putty and rod? Remember that angular velocity is a vector.
of the putty and rod? Remember that angular velocity is a vector.
(d) [6 pts] Suppose that after hitting the rod the putty did not stick but instead continued traveling in the same direction with speed
![]() . Find the angular velocity of the rod in this case.
. Find the angular velocity of the rod in this case.
6. A cart of mass ![]() is released from a height
is released from a height ![]() such that it just makes the loop of radius
such that it just makes the loop of radius ![]() as shown. After the loop the cart slides off of the end of the track which is a distance
as shown. After the loop the cart slides off of the end of the track which is a distance ![]() above the ground. The track is frictionless. Where appropriate, express your answers in terms of
above the ground. The track is frictionless. Where appropriate, express your answers in terms of ![]() and
and ![]() .
.
![\includegraphics[clip]{fig6.eps}](img39.gif)
(a) [6 pts] Find the initial height ![]() .
.
(b) [4 pts] What is the speed of the cart after completing the loop?
(c) [4 pts] Find the distance ![]() where the cart lands.
where the cart lands.
(d) [6 pts] Label a two-component coordinate system for the cart's motion after the end of the track. For each component sketch the position, velocity, and acceleration versus time.