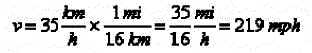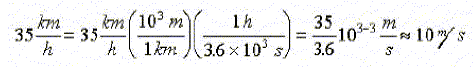HOMEWORK 3
SOLUTIONS

1: Kids in the Back!

If the car begins stopping, the child will keep going. If the car stops quickly, the child will still be going at 35 km/h and will hit the dashboard at that speed. If the car stops completely before the child hits the dashboard it will hit at 35 km/h. If the car hasn't stopped yet, the speed will be the difference between 35 km/h and the car's speed when the child hits. To do this, I need to estimate how far I will go before I stop from my driving experience. But my experience is in mi/h not km/h so I have to convert. Since 1 mile = 1.6 km, 35 km/h is equal to



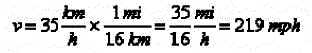
less than 30 mph, not a very high speed. I expect I can stop in about 50-100 feet. Let's call it 50 ft. We could work out exactly how fast the car was going when the child hits the dashboard, but it's fairly tedious. Let's assume you've really jammed on your brakes and things go flying forward (i.e., keep going at the speed they were going) and that you're almost fully stopped when they hit. This will be a bit of an overestimate (perhaps 20-30%). The world's fastest runner runs at about 10 m/s. Converting km/h to m/s is easy if we multiply by the right "1's":



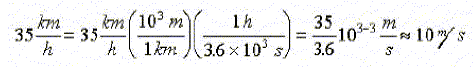
So the child hitting the dashboard is similar to the world's fastest runner running into a fixed dashboard (or worse, the windshield) while running as fast as he can.

2: Tapping a Rolling Ball

From measuring the x -spacing of the dots, it seems like the x velocity slows a bit. We note that both x and y values start positive at t = 0. We draw the position graphs first and then extract the velocity graphs by consistency and the force graphs from that using that net force is proportional to acceleration.

3: Free fall acceleration

The first statement is not really relevant since the book refers to "free-fall." This doesn't just mean "dropped." Rather, it means "there are no other forces other than gravity acting on the object" (or better, other forces acting on the object are much less than gravity and can be ignored). In the case of the balloon and feather, the force of gravity is very weak since the objects are very light. Furthermore, they are not small, so air resistance is important and cannot be ignored. For a brick, unless it is traveling at hundreds of miles an hour, air resistance can be ignored.

Therefore, this observation does not invalidate the quoted statement.

The second statement is not relevant. The statement says objects in free fall accelerate downward, not that they move downward. This refers only to how the object's velocity changes. If the object has a sideways velocity and that sideways velocity is unchanged, it does not contribute to the acceleration. The object's downward velocity increases, so the acceleration points downward. This observation, therefore, does not invalidate the quoted statement.

The third objection is conflicted. The first part of the statement is correct, as you can easily test by holding the two balls in your hands. The last part of the statement is wrong. By a = F/m, a more massive objects needs more force than a light object to get the same acceleration. The quoted statement therefore holds up despite the three objections.


4: The Sliding Pizza

We can think about the motion of the pizza box in terms of Newton's second law. If the box is to change its velocity, there need to be forces acting on it. Since we are only talking about horizontal motions (sliding to one side or another) the forces that affect these motions must be touching forces. There must be something touching the box to change its motion.

When I am turning left, the car and the pizza box are moving forward in a straight line before the turn begins. To change the velocity so it turns left or right, something must push or pull the box to the left or right while the car is turning. The box is touching the cowl of the steering wheel and the dashboard. The cowl of the steering wheel can only push to the right, not pull the box to the left. The dashboard can exert friction in any direction, but this isn't very big and may not be enough to change the box's velocity. So when I turn to the left, the box wants to go straight. As the car turns under it, there is nothing that can push the box to the left so it may slide (apparently moving right to the driver moving to the left with the car), trying to continue going straight. When I turn to the right, the cowl of the steering wheel can press against the box, pushing it to the right and keeping it moving with the car. So I have to worry when turning left, not right. (This is easy to see in your mind's eye if you imagine yourself a bird flying above the car and that the car is a convertible with its top down. The box tries to go straight while the car turns under it.)

When I start, the box wants to stay where it is. To get it moving, something has to push it. But there is nothing touching it from behind that can push it forward, so it will tend to slide back onto the seat. When I stop, the box is moving and tends to keep going as the car stops. The box will then hit the windshield so the windshield will exert a backward force on it, stopping the box. I therefore have to worry most when starting, not when stopping.

5: Why bother with N1?

Our everyday experience does not contradict N1. When we think about trying to move an object ourselves, we are focusing on the force we have to exert rather than the forces the object feels. N1 only says an object will move at a constant velocity if nothing acts on it. Remembering that we are looking for physical forces (not common speech "forces"), any object can exert a physical force on another object when they touch. Mostly, objects slow down because they are touching other objects, and those other objects exert frictional forces on them.