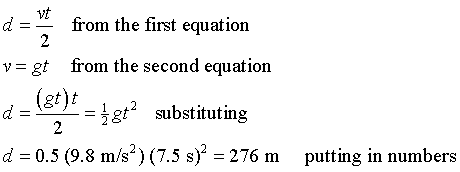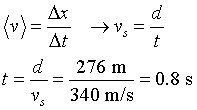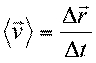HOMEWORK 2
SOLUTIONS

1. Hitting a bowling ball

(a) C You can't tell. It's been traveling for a while on both sides of the origin. The fact that the velocity is positive only tells which way it's going, not where it is.

(b) L The velocity at the instant of time marked B is negative so the ball is moving in the negative direction, to the left.

(c) R The area under the velocity curve gives the displacement. Between A and C there is more area above the line, representing a displacement to the right, than below the line, representing a displacement to the left.

(d) R After the hit at D the velocity is still positive so the ball continues to move right.

2. Waking the Balrog

(a) We start with our general foothold equations and then apply them to this specific case. We ignore air drag so the rock would fall with a constant acceleration = g = 9.8 m/s2. We assume that he just drops it -- so the initial velocity is zero. We don't know the final velocity but we're going to need it -- at least in some intermediate steps -- so let's give it the name v. Let's call the total distance the object falls d and the time it took to fall t. Here's how we start with our foothold equations and process them into an equation relevant to our problem.



Note that the "high school physics equation v=d/t" doesn't work here. That's why we use our foothold equations rather than the special case equations learned in high school (and given in our text -- unfortunately). Our foothold equations always work and contain in them (through the "average" and "change" symbols) reminders to specify exactly which velocity and distances we need to use. Note that we put our special case symbols in and then extracted two clean equations so we could see how to work with them. Otherwise there would be too many symbols, many of them standing for the same thing.

Now we can decide what we know and what we want to find out. We are given the time, t, we know the acceleration, g, and we want to find the distance d. The (final) velocity is extra. We needed it to get the equations, but we don't need to know what it is. We can eliminate it. There are two strategies to solving the problem at this point: Manipulate the symbols to get the answer for the quantity we are seeking in terms of the knowns and then substitute numbers, or put in the numbers [with units!] right away and then solve any equation that has only one unknown until we have all the answers. The latter approach will result in our finding out the final velocity as well, but will become messier if we have two equations with two unknowns, neither one of which only involves one unknown. You get to choose. In this case, it doesn't matter much. I always prefer to solve in symbols first since then I can check dimensions and limiting cases to be sure my answer makes sense.



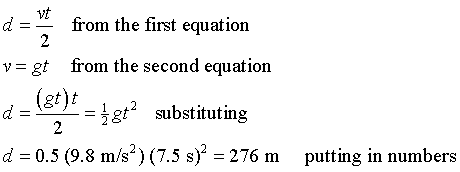
The dimensions and units check out and the answer seems reasonable.

(b) If we assume that the answer we got the last time was about right even including sound travel time, we can calculate the time the sound would take to get back up. If that is small compared to 7.5 s we are probably OK. The time for sound to travel (at a constant speed) for 276 m is given by our first foothold equation:



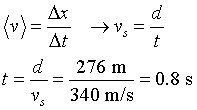
This is more than 10% of the fall time. Furthermore, the distance we calculated is proportional to the square of the time. This makes the effect of a small change in the time bigger (about twice as big). So we would expect our distance to be wrong by about 20%. If this is too much, we really need to take the time of sound travel into account. This means that the observed time includes both the time of fall and the time of sound travel time. We wind up with three equations and three unknowns -- a somewhat harder problem! Try it if you are interested.

3. Running in circles

(a) On the figure, her instantaneous velocity is her instantaneous speed pointed in the appropriate direction. Her speed is constant and is equal to the total distance, d, run over the time it took her to do it: v = Δd/ Δt = 2πr /40 s = 4.7 m/s. At A her velocity is 4.7 m/s in the upward (on the figure) direction, at C is 4.7 m/s pointing downward.



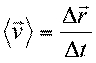
To get her average velocity, we need to get the vector displacement using the equation

Taking the origin at the center of the circle, her original position is (-30 m, 0) and her final position is (30 m, 0). Her displacement is final position minus original, or the vector (60 m, 0). Her average velocity is displacement divided by time interval -- 20 seconds for a 1/2-lap, or (3.0 m/s, 0).

(b) Her speed is constant so the average is 4.7 m/s as calculated above. Her average velocity is zero since she has no total vector displacement, i.e., initial position = final position. This average goes to zero because her velocity keeps changing direction. Although the average speed is not zero, the "average direction" is. That is, her velocity points in every direction for equal amounts of time so they all cancel out.

(c) It's bigger. If her time to complete a loop is T, from A to C she had a displacement of 2R in a time of 20 s. From A to B she had a displacement of greater than R (square root of 2 times R) in 10 s.

(d) Since she's running to cover a certain cumulative distance over a certain time, the direction doesn't really matter so average speed is probably more interesting and relevant in this example. From her speed, she could calculate her pace, a relevant measure used to evaluate runners. Average velocity is relevant over some time interval when we are interested in the forces producing a motion, since forces are associated directly with changes in velocity rather than changes in speed.

4. Tailgating

A. Different students will of course get different answers to this, but about one second is not a bad estimate for the total reaction time.

B. Let's do this one in English units because they're more familiar to American drivers. 60 mph is equivalent to 88 ft/sec. (That's a handy conversion to remember for car problems.) Reducing that velocity to zero in 5 seconds yields a (negative) acceleration of magnitude -17.6 ft/sec2. The average velocity of the car in front of you over the 5 second stopping interval is 30 mph, or 44 ft/sec. During the 5 seconds it will thus cover 220 ft.

C. Both cars are initially moving at the same speed and decelerate (accelerate in the negative direction) with the same magnitude. The following car (with you in it) will thus travel 220 ft while braking, plus 88ft additional during your one second reaction time, for a total of 308 ft. The minimum possible inter-car length that will bring you to a stop right at the leading car's back bumper is the 88 ft distance you travel in your estimated one-second reaction time. That's about 6 car lengths. A safety factor of two would be prudent, or about 12 car lengths. If you're using a cell phone, I'd advise 18-20 car lengths.

5. Racing model cars

(a) If a racecar is moving at a constant speed, according to <v>=Δx/Δt, it must go the same distance in every time interval of the same size. So in each second, it must displace by the same amount. Yellow and blue each do so, yellow by 11 m in each second and blue by 9 m in each second.

(b) Yellow has the largest velocity at t=8 s. For the constant speed cars, yellow and blue, we can get the velocity by taking displacement / time interval = 11 m/s for yellow, 9 m/s for blue. For the cars that are speeding up, we can get a good idea of their instantaneous velocity at t=8 s by looking at their average velocities in the time intervals from 7-8 s and 8-9 s. The velocity at 8 s should be the average of those two. For the red car, the average velocities in the seconds before and after t=8 sec are 6 m/s and 8 m/s, so the velocity at 8 s is probably 7 m/s. For the green car, the average velocities in the seconds before and after t=8 sec are 5 m/s and 6 m/s, so its velocity at 8 s is probably 5.5 m/s.

(c) To get an acceleration, we need to look at a change in velocity. For the green car, the velocity in the second before t=8 sec is 5 m/s and in the second after t=8 it is 6 m/s. If we assign these velocities to the middle of the 1 sec time interval, we get the velocity at t=7.5 s is 5 m/s and the velocity at t=8.5 s is 6 m/s. This gives us a change in velocity of 1 m/s in a time interval of 1 second, so we calculate an acceleration of 1 m/s/s.