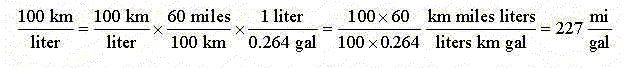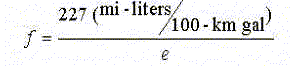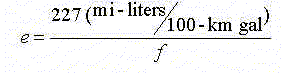1. Feeding the Cougar

This is a poser. Let's consider the issue of the food first. If you were a zookeeper or a veterinarian I just can't imagine that you would measure a big cat's food to a tenth of a gram. For one thing, each cat is a slightly different size. Second, the cat might or might not eat everything you put out. It can't possibly matter whether there's an extra few cubic centimeters or less. We might consider some possibilities:

· That the cat's food comes in a particular container and that is its size.
· That this particular cat has a carefully controlled diet for weight purposes.
· That the person writing the sign has been careless in constructing it.

The first doesn't seem plausible. Why would a food container come in such strange values? The second doesn't work for me either. You aren't likely to be able to get the cat to eat that exact amount. Anyway, if the exactness of the amount were that important (5 significant figures), then it probably depends on the cat's weight and that would change by a bigger fraction than 1 part in 10⁵ each week, so the figure wouldn't be fixed. The last seems most likely, but why should being sloppy lead to a very accurate figure?

My hypothesis is that the person making the sign asked the zookeeper how much food the cat was fed and got a report in pounds. The sign maker was told that the report had to be in metric. He then converted using the exact conversion value and kept all the values his calculator gave. Let's try this out. I know that 1 kg corresponds to (not "equals" -- mass and weight are not quite the same thing, though we can treat them as if they were as long as we remain on the surface of the earth) about 2.2 pounds. This would make the weight reported (1.3608 kg) (2.2 lbs/kg) = 2.99376 lbs. This is about 3 pounds. Suppose the reported value was 3 pounds and the sign maker converted to get 1.3608 kg. This would mean that the conversion factor used would have been (3 lbs)/(1.3608 kg) = 2.2045855... lbs/kg. This is pretty close to the number I remembered. If this is the factor the sign maker used, what would have been an average weight for the cat? (90.72 kg) x (2.2045855... lbs/kg) = 200 lbs exactly. (I didn't truncate the number in my calculator. I just kept it and multiplied by 90.72) This strongly supports my hypothesis: that the reported numbers are 3 lbs and 200 lbs. Note the different messages sent to the reader that "3 lbs and 200 lbs" sends compared to "1.3608 kg and 90.72 kg". The latter implies a much greater accuracy in the measurements. A more correct conversion should have reported "about 1.4 kg and about 90 kg".

2. Fuel Efficiency

The American efficiency is (distance traveled)/(amt. of gas used). The European efficiency is (amount of gas used)/(distance traveled). So they are basically just the reciprocal of each other with the units corrected. It would be easier to write the equation first and then we could just plug in to get the first two answers. Let's try doing it this way.

(c) The reciprocal of the European efficiency has units (100 km) / (liters). So I need to multiply by "1" in such a way as to convert 100 km to mi and liters to gallons. Since 1 km = 0.6 mi, 100 km = 60 mi so 1 = (60 mi) / (100 km). When I multiply by this form of "1" the 100 km in the numerator will cancel the 100 km in the denominator. Furthermore, looking it up, I find 1 liter = 0.264 gal. Therefore, 1 = (1 liter) / (0.264 gal). The whole calculation gives (pay attention to which terms are on top and bottom looking for what unit cancellations we need!)


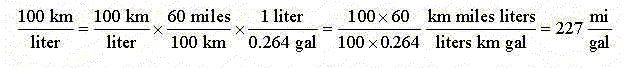
Our conversion equation is then

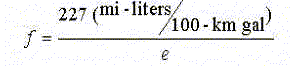
(b) If e = 7 liters/100 km, then using our formula, f = (227/7) mi/gal = 32 mi/gal.

(a) For this part we have to solve for e. We get

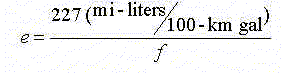
so plugging in gives e = (227/24) (liters/100 km) = 9.5 liters/100 km. Look how nicely the units work out in both cases!

3. Finding a mistake using dimensional analysis

Even though we have no clue what this calculation is about, we can check it very quickly using dimensional analysis. The problem asks us to begin by checking the final equation. Here are the dimensions of the last equation in the calculation:

(L/T²)(L) = (L/T)² +(L/T)⁴

Combining units gives:

L²/T² = L²/T² + L⁴/T⁴

Notice that when we are looking a dimensions, the numbers out front don't matter since they have no units. We are only checking to see if we are using the same kind of quantity. So if we were adding two velocities, we would write

L/T = L/T + L/T

and this would be correct. (No "2" is needed.) What it is saying is: a velocity can be added to a velocity. The result is still a velocity.

In our case, clearly the L⁴/T⁴ term is likely to be the wrong one since the other two terms match. You can't add something that has dimensions L²/T² to something that has dimensions L⁴/T⁴ and get a sensible result, so however it was derived, the last equation has to be wrong. <P< are:

(M)(L/T²)(L) = (M) (L/T)² (L) + (ML²) (1/T)² ML²/T² = ML²/T² + ML²/T².

This works. Our analysis says that the two quantities on the right side of the starting equation are of the same type, so it is OK to add them together. Once we have done so, we get another quantity of the same type.

Can we find the mistake? Since we know the first equation is dimensionally OK (it still could have wrong coefficients or not apply to the situation we are trying to apply it to, but at least it is properly formed), we only have to compare the terms that change. Replace I by MR² is dimensionally OK. Both give dimensions of ML². Replacing w by v²/R is NOT OK because w has dimensions 1/T while v²/R has dimensions (L/T)²/L = L/T², so that's the error, whatever these quantities mean.

4. Scaling Up

(a) The simpler problem we might tackle is to consider her making a simpler sculpture than Testudo -- say a cube. (We could imagine that she is doing a modernistic version and incising small lines on the cube so as to give it the apparent shape of a terrapin. Perhaps she is "making a statement.") For a cube multiplying each dimension by 5 means that the volume increases by a factor of 5x5x5=125. Since the bronze is bought by volume, she must buy 125x2 kg = 250 kg.

For the varnish, she has to cover 6 sides of the square. If the original square had a side a, the area she has to cover is 6a². This requires 2 cans of varnish so each can can cover an area 3a². When she multiplies her dimensions by 5 each side has an area (5 a)x(5 a) = 25 a². There are 6 sides, so the total area is 6 x 25 a² = 150 a². Since she needs one can to cover an area 3a² with two coats she will need 25 cans -- 25 times as many as before. If we assume she only gives it one coat, she will need 12.5 cans worth of varnish so she will have to buy 13 cans.

Now what about a more complex terrapin shape? If you imagine the terrapin now made up of small cubes, it's clear that when you scale up, the amount of bronze for each little cube scales up by a factor of 125 and the area of each side of the little cube scales up by a factor of 25. We can choose our cubes smaller and smaller until we have essentially a perfect terrapin and the factors are still 125 and 25.

Of course you can see this much more easily by using dimensional analysis. We know that a volume has the dimensions of the cube of a length ([volume] = L ³ ). If we scale the length by some factor (say 5), then the volume scales by the cube of that factor, or 125. We know that an area has the dimensions of the square of a length ([area] = L²). If we scale the length by some factor (say 5), then the volume scales by the square of that factor, or 25. And that will be true for any shape at all.

(b) To decide what the effect of convolution is, let's suppose that the human brain were not convoluted. How much bigger would it's surface area be than a mouse's brain? We can then suppose that the remaining factor is due to convolution, What we learned from the previous problem is that because of its dimension (L²), area scales as the square of the linear dimension. That is, if we increase all linear dimensions of an object by a factor x, then its area increases by a factor x² (and its volume increases by a factor x³).

We therefore only need to know how much the linear dimension is increased in going from a mouse to a human brain. (Assuming they otherwise have about the same shape.) This really depends on which mouse and which human you choose. All of them are not the same. The statement in the problem came directly from Science magazine, but they did not specify anything more. To really solve this problem, we would need to know not only the average size of human and mouse brains, but how much they vary from sample to sample (the expected range of variation). Since we don't have that info, let's try to do the best estimate we can.

Measuring my head from front to back, I expect my brain has a length of about 15 cm. Thinking about the size of a mouse's head and looking at my ruler, I estimate that a mouse's brain has a length of about 1 cm. This says that the linear size of a human brain is about 15 times that of a mouse's so x = 15 and the human brain area would be about x2 = 15x15 = 225 times the mouse brain area. This would say that the convolutions account for a factor of 1000/225 or about 4. That is, the convolutions of the human brain give it about four times the area one might expect from size alone.

How good are these numbers? I just made them up, after all from looking at a ruler and thinking about my head and a mouse. Looking on the web, we find data to suggest that the average mass of a human brain is about 1500 grams and the average mass of a mouse brain is about 0.4 grams. Since the mass should be proportional to the volume with a constant (the density -- assuming that all brains are made of about the same stuff and therefore have the same density) the mass should scale like x³ where x is the linear increase in size from human to mouse brain. That is,

Mhuman = x³ M mouse

Solving this for x gives

x= [Mhuman/ Mmouse] ^1/3 = (1500/0.4)^1/3= 15.5

Very close to the number from my estimate, so my estimate is probably pretty good! For more info on this stuff, check out the website at http://serendip.brynmawr.edu/bb/kinser/Home1.html.

5. Byting the Disk

Using the first digit of my thumb to measure, I find that a typical floppy disk is about 2.5 inches on a side. This is about (2.5 in) x (2.54 cm/in) or about 6 cm. I know that there is a circular disk inside so it has a radius of about 3 cm. This implies an area of πr² = about 3 x 3 cm x 3 cm or about 30 cm². The floppies I use hold 1.44 MB of information. This is 1.44 x 10⁶ bytes = 1.44 x 10⁶ bytes x (8 bits/byte) = about 10⁷ bits. These bits are distributed over an area of 30 cm² (= 30 x 10^-4 m² = 3 x 10^-3 m²) so, assuming that each bit has its own space and there is no overlap, each bit must occupy a space of (3 x 10^-3 m²) / (10⁷ bits) = 3 x 10^-10 m². If we think of this as a tiny square, it has dimensions Sqrt(3) x 10^-5 m or about 15 micrometers on a side.

Computers process things in terms of strings of digits, each of which can have only one of two values, zero or one. For example 1011 might represent the number that this translates into in our usual number system (eleven), or it could be used to represent a letter or a comma or something else. If one wants to be able to represent all the letters of the alphabet, both upper and lower case, plus all the numerical digits from zero to nine, plus some other useful things like punctuation marks, each with a different binary number string, how long must the binary number strings be? Well, if I count the associated keys on the computer keyboard in front of me, I find about 130 items I'd like to represent, each with a different binary number string. Now, if each string is n binary digits long, the total number of different binary numbers available for representing things is 2ⁿ. It is then obvious that n=8 would give us enough numbers to represent everything on a typical keyboard and also provide some leeway to cover some additional internal computer needs as well. One might think of a string of eight bits as the appropriate size of the bundle of binary digits necessary to represent letters of the alphabet and other useful things. It's always nice to have a name for bundles of things, and so we have "byte" for a bundle of eight bits. I don't know how that name was invented, but you have to admit it's cute.