Remarks about Gravity Chapter

• Kepler's laws apply to elliptical orbits, if instead of the radius r you use half the largest diameter of the ellipse (the "semimajor axis"). Even if the orbit is a radial line.

  Example: how long does it take to fall, from rest, from the earth's orbit to the sun?
  Answer: Half the period of the "elliptical" orbit, whose major axis is the earth-sun distance R, so the semimajor axis is R/2. We know T²/r³ is the same for the earth and the falling object, so

  (1 year)²/R³ = t²/(½R)³; solve: t = (1/8)^½ yearhence falling time = t/2 = 0.177 year
• Because the force of gravity decreases with distance sufficiently rapidly, it takes only a finite amount of energy, and a finite initial speed, to get arbitrarily far away from a gravitationg body. For the earth this speed is about 10 km/s.
• "funnel" model of a gravitational field should be taken with a grain of salt.
  

Comparison of linear and angular quantities

linear	angular	relation
position r	angle q	arclength s = r q
velocity v	angular speed w	v = r w
acceleration a	angular acceleration a	a = r a   1
constant a: Dr = v t + ½ a t²	constant a: Dq = w t + ½a t²
Force F	Torque t	t = rp F   2
mass m	moment of inertia I	I = S mr²
momentum p = m v	angular momentum L = rp mv For rigid body rotating about fixed axis: L = I w	L = S rp p
Newton: F = Dp/Dt = m a	t = DL/Dt = I a
K.E. of translation:   ½ m v²	K.E. of rotation   ½ I w²	total K.E. = K.E. of translation of C.M. + K.E. of rotation about C.M.
Equilibrium: S F = 0	S t = 0	Both for a rigid body

¹This is tangential acceleration. Radial acceleration = v²/r = r w²
² r_p is the perpendicular distance to the "line of action" of the force resp. the velocity or momentum. Equivalently one could write this as r F_p, where F_p is the component of F perpendicular to r.

• For a system of bodies you can use the linear Newton's law for some, and angular "Newton's law" for others, as appropriate.³
• Forces applied at the (momentary) center of rotation exert no torque, do not change angular momentum
• Usually K.E. of translation and of rotation are not separately conserved; both appear in the conservation of total energy, for example: ½ m v² + ½ I w² + mgh = const

³ Example of use: Atwood's machine (Text Figure P4.34, p. 109) with a pulley a disk of mass M and radius R, hence moment of inertia I = ½MR². What is its acceleration?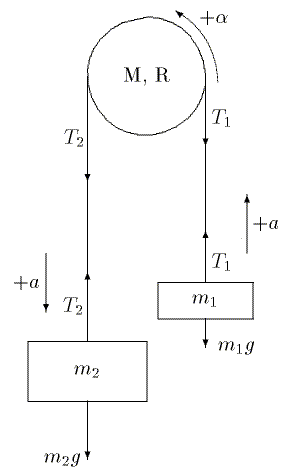
So that we do not have to introduce separate accelerations of the three bodies we choose the positive direction as indicated, then the accelerations of the two loads and that of the pulley's rim are equal.
We do have to introduce different tensions T₁, T₂ on the two sides of the pulley, so that a torque can be exerted on the pulley.
By isolating the bodies we find

(linear) Newton's law for m₁:   T₁ - m₁ g = m₁ a

(linear) Newton's law for m₂:   m₂ g - T₂ = m₂ a

Rotational law for pulley:   T₂ R - T₁ R = Ia = ½MR² (a/R)

Cancel an R and substitute for the tensions: