| your name: _______________________ |
| Physics 121 |
Second Exam | November 16, 2006 |
Instructions: This exam consists of 5 pages, including this cover sheet. Put your name on all 5 pages. Answer all three questions on these sheets.
Problem I (36 points, 2 per question) is standard multiple-choice, graded only by chosen answer (work needs not be shown). Read problem carefully, it may differ by a few crucial words from what you may have seen before!
For Problems II and III (32 points each) it is important to show your method or reasoning clearly. In any case, leave no doubt which of possibly several numbers or formulas is your final answer -- for example by drawing a box around it.
Use the back of a previous page for scratch work.
The exam lasts 60 minutes. Please hand in all four pages of your paper according to the initial letter of your last name, using the alphabetical trays, except section SEF1 which will have a separate box.
Copy and sign the pledge below:
I pledge on my honor that I have not given or received any unauthorized assistance on this examination.
I. Multiple Choice Mark your answer in a column on the right, -- in other words, here ¯
- A particle orbits about a center C, held in orbit by an attractive, radial force. The power
delivered by the force vanishes at all points of the orbit under what conditions?
a. always b. only if the force is conservative c. only if the orbit is circular d. never
- A golf ball hits a wall and bounces back at 1/2 the original speed. What part of the original
kinetic
energy of the ball did it lose in the collision?
a. 1/4 b. 1/2 c. 3/4 d. all of it
- When an object is dropped from a tower, what is the effect of the air resistance as it falls?
a. does positive work b. increases the object’s kinetic energy
c. increases the object’s potential energy d. None of the above choices are valid.
- A 2.00-kg ball has zero potential and kinetic energy. Ernie drops the ball into a 10.0-m-deep well.
After the ball comes to a stop in the mud, the sum of its potential and kinetic energy is:
a. zero. b. 196 J. c. -196 J. d. 392 J.
- A Hooke’s law spring is mounted horizontally over a frictionless surface. The spring is then
compressed a distance d and is used to launch a mass m along the frictionless surface. What
compression of the spring would result in the mass attaining double the speed received in the
above situation?
a. 1.41 d b. 1.73 d c. 2.00 d d. 4.00 d
- A billiard ball collides in an elastic head-on collision with a second identical ball. What is the
kinetic energy of the system after the collision compared to that before collision?
a. the same as b. one fourth c. twice d. four times
- A 5-kg object is moving to the right at 4 m/s and collides with another object moving to the left at
5 m/s. The objects collide and stick together. After the collision, we can be sure that the combined object:
a. is moving to the right. b. is moving to the left. c. is at rest.
d. has less kinetic energy than the system had before the collision
- Consider a point on a bicycle wheel as the wheel turns about a fixed axis, neither speeding up nor
slowing down. Compare the linear and angular accelerations of the point.
a. Both are constant. b. Only the angular acceleration is constant.
c. Only the linear acceleration is constant. d. Neither is constant.
- Consider a child who is swinging. As she reaches the lowest point in her swing:
a. the tension in the rope is equal to her weight.
b. the tension in the rope is equal to her mass times her acceleration.
c. the tension in the rope is equal to the sum of the magnitudes of a. and b..
d. none of the above.
- A wheel is rotated about a horizontal axle at a constant angular speed. Next it is rotated in the
opposite direction with the same angular speed. The acceleration vector at a point on the bottom of the
wheel in the second case as compared to that vector in the first case:
a. is in the same direction. b. is in the opposite direction.
c. is downward. d. is tangential to the wheel.
- At what location does the Earth in its orbit around the sun have its greatest speed?
a. nearest the sun b. farthest from the sun
c. at solstice d. the earth's speed never varies
- The Earth’s gravity exerts no torque on a satellite orbiting the Earth in an elliptical orbit.
Compare the motion of the satellite at the point nearest the Earth (perigee) to the motion at the point farthest from the Earth (apogee). At these two points:
a. the tangential velocities are the same. b. the angular velocities are the same.
c. the angular momenta are the same. d. the kinetic energies are the same.
- A 4.2-kg mass is placed at (3.0, 4.0) m. Where can an 8.4-kg mass be placed so that the moment
of inertia about the z-axis is zero?
a. (-3.0, -4.0) m b. (-6.0, -8.0) m c. (-1.5, -2.0) m
d. There is no position giving this result.
- A bowling ball has a mass of 7.0 kg and a radius of 0.10 m. If it rolls down the lane without slipping at a linear speed of 4.0 m/s, what is its angular speed?
a. 0.80 rad/s b. 10 rad/s c. 7.0 rad/s d. 40 rad/s
- A cylinder (I = MR2/2) starts at height 5 m and rolls down to the ground. It then comes to a hill and starts going up. Assuming no losses to friction, how high does it get before it stops?
a. 1.2 m b. 2.4 m c. 3.6 m d. 5.0 m
- Which experiment demonstrated the effects of a changing moment of inertia?



 a. b. c. d.
a. b. c. d.
- What did the scale in picture a. measure?
a. torque b. centrifugal force c. centripetal force d. angular velocity
- The experiment on the ballistic pendulum was supposed to show
a. conservation of energy b. conversion of spring energy into kinetic energy of a "bullet"
c. an elastic collision d. the measurement of the speed of a "bullet"
II. Short Answer
The picture is meant to show a disk (A) with a string wrapped around it in yoyo fashion, and, for comparison, a similar disk (B) with a string attached at the top. The mass, radius, and moment of inertia of either cylinder is M, R and I = ½MR² respectively.
The strings are fixed to the ceiling on top, and gravity g is acting. Express your answer in terms of these symbols and the height h above the floor.
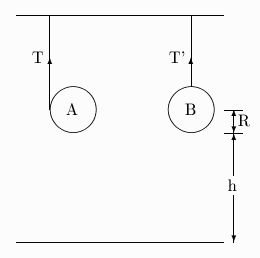
- The yoyo is released from rest, and the string of disk B is cut, so they both descend to the floor, a distance h. Just before they hit the floor, what is the total kinetic energy
of the yoyo A?
Mgh
and of the disk B?
Mgh
- What fraction of the total energy is rotational
for yoyo A
1/3 (¼MR²ω² vs ½Mv²+¼MR²ω²)
and for disk B?
0 (the disk is not rotating)
Back to the case shown in the picture where disk B is not moving because it is held up by a string; but the string wrapped around yoyo A is not fixed at its upper end, instead it is pulled up with constant acceleration in such a way that the center of the yoyo also does not move (but it starts spinning faster and faster)
- What is
the tension T' in the string that holds up the disk B?
T' = Mg
and, therefore, the tension T in the yoyo string?
T = Mg (from force balance, since center of yoyo does not accelerate)
- What is the angular acceleration α of the yoyo (in terms of T and I)?
τ= TR = Iα therefore α = TR/I
III. Tutorial question (click)




