Instructions: Answer all four questions on these sheets.
Problem I (40 points) is standard multiple-choice, graded only by chosen answer (work needs not be shown).
For Problems II - IV (20 points each) show your work, including any equations you used, or explain in words how you arrived at numerical answers.
The exam lasts 110 minutes. Please hand in all five pages of your paper according to the initial letter of your last name, using the alphabetical trays.

I. Multiple choice. Mark your answer in the boxes on the right.

I use a rope 2.00 m long to swing a 10.0-kg weight around my head. The tension in the rope is 20.0 N. In half a revolution how much work is done by the rope on the weight? a. 40.0 J         b. 126 J         c. 251 J         d. 0	d
The work done by static friction can be: a. positive.         b. negative.         c. zero.         d. Any of the above.	d
As an object is lowered into a deep hole in the surface of the earth, which of the following must be assumed in regard to its potential energy? a. increase         b. decrease         c. remain constant         d. cannot tell from the information given	b
A 2.00-kg ball has zero potential and kinetic energy. Maria drops the ball into a 10.0-m-deep well. After the ball comes to a stop in the mud, the sum of its potential and kinetic energy is: a. zero.         b. 196 J.         c. −196 J.         d. 392 J.	c
Two blocks are released from the top of a building. One falls straight down while the other slides down a smooth ramp. If all friction is ignored, which one is moving faster when it reaches the bottom? a. The block that went straight down.           b. The block that went down the ramp.         c. They both will have the same speed.         d. Insufficient information to work the problem.	c
A Hooke's law spring is compressed a distance d and is used to launch a mass m vertically to a height h above its starting position. Under double the compression, the spring is now used to launch the mass. How high does the mass now rise above its starting position? a. 2 h         b. 1.41 h         c. 3 h         d. 4 h	d
A speed boat requires 91 kW to move at a constant speed of 14 m/s. What is the resistive force of the water at this speed? a. 2 700 N         b. 5 300 N         c. 6 500 N         d. 7 700 N	c
A ball with original momentum +4.0 kg m/s hits a wall and bounces straight back without losing any kinetic energy. The change in momentum of the ball is: a. 0.         b. 4.0 kg m/s.         c. 8.0 kg m/s.         d. −8.0 kg m/s.	d
I drop a 60-g golf ball from 2.0 m high. It rebounds to 1.5 m. How much energy is lost? a. 0.29 J         b. 0.50 J         c. 0.88 J         d. 1.0 J	a
If the momentum of an object is tripled, its kinetic energy will change by what factor? a. zero         b. one-third         c. three         d. nine	d
An object of mass m moving at speed v strikes and object of mass 2m which had been at rest. The first object bounces backward along its initial path at speed v. Is this collision elastic, and if not, what is the change in kinetic energy of the system? a. The collision is elastic.                                 b. The kinetic energy decreases by mv²         c. The kinetic energy decreases by ½mv²         d. The kinetic energy increases by mv²	d
A billiard ball collides in an elastic head on collision with a second identical ball. What is the kinetic energy of the system after the collision compared to that before collision? a. the same as         b. one fourth         c. twice         d. four times	a
A point on the rim of a 0.30-m-radius rotating wheel has a tangential speed of 3.0 m/s. What is the tangential speed of a point 0.10 m from the center of the same wheel? a. 1.0 m/s         b. 1.3 m/s         c. 2.7 m/s         d. 8.0 m/s	a
Consider a point on a bicycle wheel as the wheel turns about a fixed axis, neither speeding up nor slowing down. Compare the linear and angular accelerations of the point. a. Both are zero.                                           b. Only the angular acceleration is zero. c. Only the linear acceleration is zero.         d. Neither is zero	b
A wheel is rotated about a horizontal axle at a constant angular speed. Next it is rotated in the opposite direction with the same angular speed. The acceleration at a point on the top of the wheel in the second case as compared to the acceleration in the first case is: a. in the same direction.           b. in the opposite direction.         c. larger in magnitude               d. smaller in magnitude.	a
A cylindrical space colony 0.98 km in radius and 30 km long has been proposed as living quarters for future space explorers. Such a habitat would have cities, land and lakes on the inside surface and air and clouds in the center. All this would be held in place by the rotation of the cylinder about the long axis. How fast would such a cylinder have to rotate to produce a 1-g gravitational field at the walls of the cylinder? a. 0.05 rad/s         b. 0.10 rad/s         c. 0.15 rad/s         d. 0.20 rad/s	b
If a net torque is applied to a rigid body, that body will experience: a. a constant angular momentum.           b. an angular acceleration.         c. a decreasing moment of inertia.         d. an increasing moment of inertia	b
A 40-kg boy is standing on the edge of a stationary 30-kg platform that is free to rotate. The boy tries to walk around the platform in a counterclockwise direction. As he does: a. the platform doesn't rotate.         b. both go around with equal angular velocities but in opposite directions. c. the platform rotates in a clockwise direction just fast enough so that the boy remains stationary relative to the ground. d. the platform rotates in a clockwise direction while the boy goes around in a counterclockwise direction relative to the ground.	d
A solid disk of radius R rolls down an incline in time T. The center of the disk is removed up to a radius of R/2. The remaining portion of the disk with its center gone is again rolled down the same incline. The time it takes is: a. T.         b. more than T.         c. less than T.         d. requires more information than given in the problem to figure out.	b
A figure skater with arms initially extended starts spinning on the ice at 3 rad/s. She then pulls her arms in close to her body. Which of the following results? a. a smaller rotational rate                 b. a greater rotational rate         c. a greater angular momentum         d. a smaller angular momentum	b

II.
Today the Johnson family is moving and the movers just arrived to load the truck. Boxes of the same mass must be moved up a ramp from the basement, and also up a ramp into the moving truck. Both ramps have negligible friction, and the vertical displacement of both boxes is the same. The mover exerts forces of the same magnitude up both ramps, in each case parallel to the ramp.

1. Mrs. Johnson assumes that the mover will do more work trying to get the boxes into the truck than out of the basement because the truck ramp is steeper. She offers Mr. Johnson's assistance with the truck ramp. Mr. Johnson assures her that since the ramps have equal height increases the mover will do the same amount of work moving the boxes over both ramps, and thus he should make himself useful somewhere else. Do you agree with Mrs. Johnson, Mr. Johnson, or neither? Explain your reasoning.
   

   Neither. Mrs. Johnson did not take into account the distance over which the force was exerted. Mr. Johnson does not take into account that the force exerted is the same in both cases. Both assume that the amount of work to be done (rather than, for example, the force to be exerted) determines where help is needed.
   This is a sufficient explanation for disagreeing with either, and it is safest to say this and no more -- both of them certainly made mistakes, or at least overlooked something.

   It is more difficult to argue what the "correct" answer is, because that depends on assumptions one must make.
   The least radical is probably that "moving a box up a ramp" has not quite the same meaning for the two ramps, namely the box may have K.E. at the end of the move from the basement, but not when it arrives in the truck. If the need for help is based on the work to be done, Mr. Johnson should then help with the basement ramp.
   However, in another interpretation of the stated condition one could note that it was never specified that the exerted force indeed is able to move the box. Maybe it is just enough to move it up the basement ramp, and then Mr. Johnson should clearly help with the truck ramp. Mrs. Johnson would be right, but for the wrong reason (The mover will do zero work on the truck ramp if by himself, since he cannot move the box; with Mr. Johnson he will do less work than on the basement ramp, but the two together will do an equal amount of work as the mover alone on the basement ramp).
   Finally, if you have a good lawyer you may be able to argue that the problem is misleading because other problems have taught you to disregard data that are not needed for the calculation (here, the comparison of the forces up the ramps), you are entitled to assume "moving up the ramp" means the same thing in both cases, and agree with Mr. Johnson.
   

   
   

2. Is the potential energy gained by Box 1 greater than, less than, or equal to the potential energy gained by Box 2? Explain.

   Equal. The potential energy gain, mgh₀ is the same because the masses and the heights are the same for box 1 and box 2.

III.
Consider this movie action scene, taking place in an abandoned mine provided with a ramp, a stationary cart on rusty but frictionless rails, overhead pipes (one of them well-greased), and an escape exit over a bottomless abyss (the escape and abyss are inessential; see figure next page):
Our hero, idealized as a thin, uniform rod initially at rest (1), slides frictionlessly down the ramp (2), and onto the cart (3). The impact makes the cart with hero roll horizontally until our hero can grab the overhead pipe (4) and let his momentum (he is not quite sure whether angular or linear) swing him up (5). He has to swing at least 90° to escape (6).
The path of his center of mass is shown by the heavy dotted curve. There is no friction between any moving surfaces, and the cart's wheels have negligible moment of inertia. If the mass of the cart equals the mass of the hero, will he make it to position 6?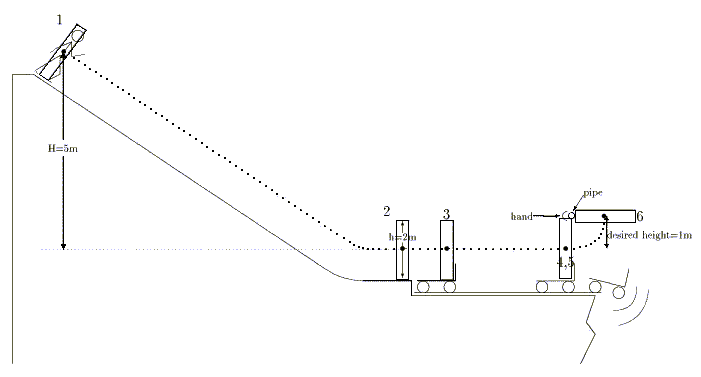

1. The answer would be easy if total mechanical energy were conserved throughout the motion. Instead we must analyze it in stages, where stage 4 is just before hero grabs the pipe, and stage 5 is just after that moment, when he is already free of the cart and just starting his upward swing. Therefore identify all the quantities that are conserved at the various stages, by marking a × or a √ in the table below (leave non-conserved quantities blank):
   

   Conserved Quantities

   stage of motion	energy (K.E.+P.E.)	linear momentum	angular momentum	origin for ang.mom.
   1 to 2	×
   2 to 3		×
   3 to 4	×	×	(×)	(pipe)
   4 to 5			×	pipe
   5 to 6	×

To answer the questions on the next page, use the following data:

height of ramp H = 5 m	hero's mass M = 100 kg	cart's mass m = M = 100 kg
hero's height h = 2 m	hero's moment of inertia about one end = Mh²/3 = 133 kg m²
height of hero's center at stage 6 = H/5 = 1 m

Your answers may be numerical or in terms of these (and only these) symbols.

2. What is our hero's speed at stage 2?

   By energy conservation, ½Mv² = MgH hence   v = √(2gH) = √(2×10m/s²×5m) = 10 m/s (using g = 10 m/s²
   

3. What is the speed of hero+cart at stage 3 and 4?

   By momentum conservation, Mv = (M + m)v' = 2Mv'   v' = v/2 = 5 m/s
   

4. What is hero's angular momentum at 5?

   By angular momentum conservation about the pipe, of the hero alone:
   Before he grabs the pipe his angular momentum is linear momentum × distance CM to pipe = Mv'×(h/2) = 500 kg m²/s = L;
   alternatively, the angular momentum is that of the CM only, since he is not yet rotating about the CM. The angular velocity ω_CM of the CM is v'/(distance CM-pipe) = v'/(h/2) = 2v'/h (= v/h) and the moment of inertia of the CM I_CM = M(h/2)², so L = I_CMω_CM = (Mh²/4)(2v'/h) = Mhv'/2 as before.
   This is really the angular momentum at 4, but since it is conserved, it is also the angular momentum at 5.

5. What is hero's kinetic energy at 6 -- or does he not make it to stage 6?

   By energy conservation, ½Iω² + Mgy = const. However, we don't yet have ω at stage 5. Hence EITHER
   (1) work that out: the above angular momentum L = I_{one end}ω' so ω' = L/I_{one end} = (500kg m²/s)/133kg m² = 3.75/s, and the initial KE is ½Iω² = ½(133)(3.75)² = 937.5 J. OR
   (2) Remember that in terms of the (conserved!) L, KE is L²/2I = (500 kgm²/s)²/2(133 kgm²) = 937.5 kg m²/s² -- same answer (15000/16). Now you would subtract from that the PE gain from 5 to 6 = Mg(H/5) = 1000 J to get the KE energy left. But KE energy can't be less than 0: our hero just barely does not make it. (But don't be sad. He actually ceased being a rigid body, flung his legs, and did make it :)

IV.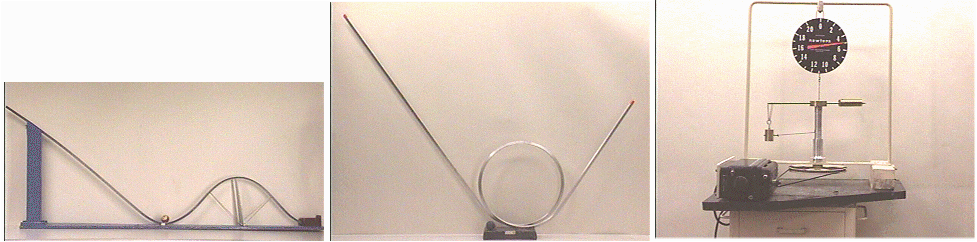

The first two photos will remind you of two rather similar demos.

1. What did the hill track demonstrate?

   Conservation of kinetic+potential energy. A rolling ball could come back to its original height, but no higher. To travel beyond (over) the hill, with possibly very small velocity, it had to start from rest at a height at least equal to that of the hill.
   

2. What did the loop-the-loop demonstrate that's different from the hill track?

   Centripetal force. The ball had to have a minimum velocity at the top of the loop. Sufficient centripetal acceleration was necessay for the ball to remain on track. (From the point of view of the observer rotating with the ball, the centrifugal force kept the ball on track in spite of gravity pulling it away)
   

3. In order that the ball can go over the hill of the hill track we had to start it only a little higher than the highest point of the hill. But to make it go through the complete loop, we had to start it considerably higher than the top of the loop. Why and how are the conditions at the top different in the two cases?

   In both cases there must be a non-negative normal force it the ball is to keep on track. On the hill track top, normal force and gravity are in opposite directions, so we can have v = 0 and cancellation of these forces. On the loop track top the two (gravity and normal) are in the same direction (down), so there must always be a centripetal acceleration.
   

The third photo is called "central force-rotating mass".

4. What did that demo demonstrate? Mention which of the masses is the active one that the experiment is about.

   This experiment showed centripetal force quantitatively. The active mass is the one on the left, which has a string attached to it that goes to the force meter
   

5. Was the photo taken when the apparatus was at rest or when it was rotating? How do you know?

   It was rotating because the centripetal force meter shows a nonzero reading.
   

6. What is the purpose of the other rotating mass shown in the photo? What condition determines its proper place, what would happen if it were not in that proper place?

   It is a counterweight, positioned so that the center of mass of the rotating part of the apparatus is on the axis of rotation, so that the centripetal force exerted on the counterweight is equal and opposite to that exerted on the active mass. If these forces were not in balance, the reaction force to their difference would shake the apparatus and prevent it from running smoothly.