Instructions: Answer all four questions on these sheets.
Problem I (40 points) is standard multiple-choice, graded only by chosen answer (work needs not be shown).
For Problem II (20 points), draw graphs so we can tell whether a line is straight or curved, horizontal or slanted, and explain your reasoning in the space provided.
For Problems III and IV (20 points each) show your work, including any equations you used, or explain in words how you arrived at numerical answers.
The exam lasts 100 minutes. Please hand in all four pages of your paper according to the initial letter of your last name, using the alphabetical trays.

I. Multiple choice. Mark your answer in the boxes on the right.

Which expression is dimensionally consistent with an expression that would yield a value for time? (v is velocity, x is distance, and t is time) a. v/x     b. x/v     c. v²/x     d. x/v²	b
The distance to the Andromeda Galaxy is estimated at about 2 × 106 light years. A light year is the distance traveled by light in one year; if the speed of light is 3 × 108 m/s, about how far is it from our galaxy to Andromeda? (1 year = 3.15 × 107 s) a. 2 × 1022 m     b. 1 × 1018 m     c. 10 × 1015 m     d. 6 × 1012 m	a
A truck moves 70 m east, then moves 80 m west, and finally moves east again a distance of 90 m. If east is chosen as the positive direction, what is the truck's resultant displacement? a. 40 m     b. - 40 m     c. 80 m     d. 240 m	c
Norma releases a bowling ball from rest; it rolls down a ramp with constant acceleration. After half a second it has traveled 0.75 m. How far has it traveled after one second? a. 1.5 m     b. 2.1 m     c. 3 m     d. 6.0 m     e. 12 m	c
A strobe photograph of a car moving along a straight road shows the interval between each successive image to be diminishing. If the direction of motion of the car is taken as positive, which of the following is/are negative? a. the average acceleration of the car         b. the average velocity of the car c. the speed of the car                    d. all of the above	a
Jeff throws a ball straight up. For which situation is the vertical velocity zero? a. on the way up     b. at the top     c. on the way back down     d. none of the above	b
A jogger runs halfway around a circular path with a radius of 100 m. What, respectively, are the magnitude of the displacement and the distance jogged? a. 200 m, 314 m     b. 120 m, 188 m     c. 0 m, 377 m     d. 60 m, 377 m     e. 120m, 188m	a
A vehicle designed to operate on a drag strip accelerates from zero to 30 m/s while undergoing a straight line path displacement of 45 m. What is the vehicle's acceleration if its value may be assumed to be constant? a. 2.0 m/s²     b. 5.0 m/s²     c. 10 m/s²     d. 15 m/s²	c
Human reaction time is usually about 0.20 s. If your lab partner holds a ruler between your finger and thumb and releases it without warning, how far can you expect the ruler to fall before you catch it? The nearest value is: a. 4.0 cm.     b. 9.8 cm.     c. 16 cm.     d. 20 cm.	d
The first displacement is 6 m and the second displacement is 4 m. They cannot add together to give a total displacement of: a. 4 m.     b. 6 m.     c. 12 m.     d. 6.4 m.	c
A ball is rolled horizontally off a table with an initial speed of 0.12 m/s. A stopwatch measures the ball's trajectory time from table to the floor to be 0.30 s. What is the height of the table? (g = 10 m/s² and air resistance is negligible) a. 0.12 m     b. 0.45 m     c. 0.90 m     d. 1.1 m     e. 1.2 m	b
The highest mountain on Mars is Olympus Mons, rising 22 000 meters above the Martian surface. If we were to throw an object horizontally off the mountain top, how long would it take to reach the surface? (Ignore atmospheric drag forces and use gMars = 3.72 m/s².) a. 1.8 minutes     b. 2.4 minutes     c. 3.0 minutes     d. 0.79 minute	a
If we know an object is moving at constant velocity, we may assume: a. a force is acting to keep it moving        b. there are no forces acting on the object. c. the object is accelerating.               d. the net force acting on the object is zero.	d
Two blocks, joined by a string, have masses of 6.0 and 9.0 kg. They rest on a frictionless horizontal surface. A 2nd string, attached only to the 9-kg block, has horizontal force = 30 N applied to it. Both blocks accelerate. Find the tension in the string between the blocks. a. 18 N     b. 12 N     c. 28 N     d. 15 N	b
An airplane of mass 1.2 × 104 kg tows a glider of mass 0.6 × 104 kg. The airplane propellers provide a net forward thrust of 3.6 × 104 N. What is the glider's acceleration? a. 9.8 m/s²     b. 9.0 m/s²     c. 6.0 m/s²     d. 3 m/s²     e. 2.0 m/s²	e
As I slide a box at constant speed up a frictionless slope, pulling parallel to the slope, the tension in the rope will be: a. greater than it would be if the box were stationary.     b. greater than the weight of the box. c. equal to the weight of the box.                    d. less than the weight of the box.	d
It is late and Carlos is sliding down a rope from his third floor window to meet his friend Juan. As he slides down the rope faster and faster, he becomes frightened and grabs harder on the rope, increasing the tension in the rope. As soon as the upward tension in the rope becomes equal to his weight: a. Carlos' speed will start to decrease.     b. Carlos will continue down at a constant velocity. c. Carlos will stop.                    d. the rope must break.	b
As a car moves forward on a level road at constant velocity, the net force acting on the tires is: a. zero. b. equal to the normal force times the coefficient of static friction. c. equal to the normal force times the coefficient of kinetic friction. d. greater than the normal force times the coefficient of static friction.	a
A block is launched up an inclined plane. After going up the plane, it slides back down to its starting position. The coefficient of friction between the block and the plane is 0.3. The speed of the block when it reaches the starting position on the trip down: a. is the same as the launching speed. b. is less than the launching speed. c. is more than the launching speed. d. cannot be compared to the launching speed with the information given.	b
The coefficient of static friction between the tires of a car and the street is µs = 1.0. Of the following, what is the steepest inclination angle of a street on which a car can be parked (with wheels locked) without slipping? a. 22.5°     b. 30°     c. 37°     d. 40°         e. 45°	e

II.
1. Pat and Kim are practicing for tomorrow's all-star basketball tryouts. Pat suggests running lines. Running a line, Pat tells Kim, means running to a line at the other side of the gym, touching it, and then running back.
a. Below is a position vs. time graph showing part of Pat's motion during one line run. Draw a qualitatively correct velocity vs. time graph of Pat's motion. Explain briefly.
The velocity is the slope of the first graph. The slope is positive at the left, zero in the middle, and negative on the right.

b. Describe and sketch how you could set up a track so that a cart (given suitable initial velocity, but no further push "by hand") would travel with the same motion as Pat's. In yoursketch, be sure to include labels* to show relevant locations and orientations.
 

The motion graph corresponds to an acceleration away from the "other side". For a cart we can simulate this motion by letting gravity provide the acceleration via a tilted track. (The motion graph looks close to parabolic, so a constant-slope incline will do)

* such as "other side", "up" etc.

2. After running a few lines, Kim suggests a long distance run. While Pat is a better sprinter, Kim has better endurance for long distances. Below is a partial graph of the motions.
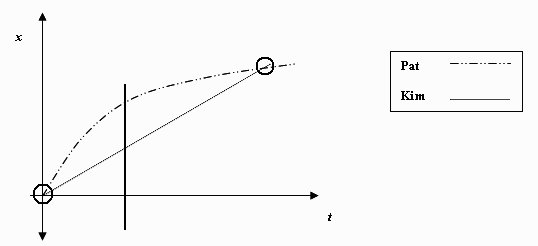a. Is there any instant during the run when Pat and Kim have the same velocity? If so, mark the instant on the graph by a vertical line through its time coordinate value, and explain your reasoning. If not, state so explicitly and explain.

The slopes of the two graphs are equal at this time.

b. Are there any instants during the run where Pat and Kim are alongside one another? If so, circle these instants and explain. If not, state so explicitly and explain.

At these instants the two graphs cross

III. A helicopter is traveling at 40 m/s at a constant altitude of 100 m over a level field. Assume g = 10 m/s² and negligible air resistance

1. If a wheel falls off the helicopter, how long does it take to hit the ground?

This concerns only the (independent) vertical motion. The initial vertical velocity is zero, so we have 100m = ½ (10 m/s²) t², hence t = (20)^½ s ~ 4.5 s

2. With what total speed will it hit the ground?

v² = v₀² + 2gy = (1600 + 2000)m²/s²   so   v = 60 m/s.

Since the horizontal motion is unchanged during the free fall, it hits the ground immediately below the helicopter.

IV. In the famous "Monkey and Hunter" lecture demonstration set-up shown at the right a "monkey" became a moving target but was hit by a "bullet" from a fixed (non-moving) "blowgun".

1. What was the point of the demonstration, what principle of physics was exhibited?

Independence of motion under gravity in two independent directions

2. Where was the "gun" aimed (if you answer "at the monkey" better specify at what time, since monkey is a moving target)

At the monkey's initial position, before he started falling

3. Where was the bullet when the monkey let go of his support and started his free fall?

4. How was the properly-timed release of the monkey accomplished in this experiment?

Upon leaving the gun, the bullet tripped an electrical switch, which cut the current to the electromagnet that was holding up the "monkey"

5. If the bullet travels too slowly, the monkey will escape being "shot". Where does the bullet then hit?

It hits the floor in front of the monkey (closer to the gun).

6. Suppose the monkey is hit half-way down to the ground (with the gun at ground level). In what direction did the bullet approach the monkey? (in words, or give v_y/v_x, or just v_y)

It comes at the monkey horizontally, that is v_y = 0. (extra credit was given for this answer)
To show this, assume the monkey is at height h, a horizontal distance D away from the gun. Then initially (t=0) v_y0/v_x = h/D. Let T be the time at which the monkey is hit, then D = v_xT and, canceling v_x in the previous equation, we have v_y0 = h/T.
The monkey falls to ½h in that time, so ½h = ½gT² substituting in above gives v_y0 = gT. At time T we therefore have v_y = v_y0 - gT = 0.