Part I   Correct answers in bold. Red answers were missed by the majority, so those are particularly worth studying.

1. Given two waves, A and B, we can bring them together and let them interfere. We can also let wave A amplitude modulates wave B.
   A difference between these two processes is
   1. in interference the waves are added (A+B), in modulation they are multiplied (A×B)
   2. interference can lead to total cancellation, modulation always yieds a non-zero wave
   3. the spectrum for interfering waves contains only frequencies in the spectrum of wave A and/or wave B, whereas the modulated wave's spectrum generally has some frequencies that are not in either wave.
   4. all of the above

2. When I add a sine wave R, going to the right, to a sine wave L, of equal amplitude and frequency but going to the left, I get a standing wave, S. Now suppose I instead subtract L from R. What will be the result?
   1. I also get a standing wave, indistinuishable from S
   2. I get a standing wave with nodes and antinodes at the same places as S, but vibrating out of phase with S
   3. I get a standing wave with nodes where S had antinodes and vice versa
   4.  I get a standing wave with nodes and antinodes in positions in the middle between those of S.

3. When two travelling waves are added and the result is a pure standing wave,
   1. the two travelling waves must have the same amplitude
   2. the two travelling waves must have the same wavelength
   3. the standing wave will have the same wavelength as the travelling waves
   4. the standing wave will have twice the amplitude of either travelling wave
   5. all of the above

4. A constraint on any possible standing wave on a rope (fixed at both ends) is
   1. there must be a node at each end
   2. all the loops of the standing wave must have equal amplitudes
   3. all the loops must be of equal length
   4. the length of each loop must be one half-wavelength
   5. all of the above.

5. A musical note that is not in the overtone series of a given fundamental frequency is related to that fundamental by an interval of
       a. one perfect fifth     b. one octave           c. one octave + one perfect fifth
       d. Two octaves         e. none of the above

6. When violin study is taken up at an early age, a "half violin" is used to accommodate a child's smaller arms. (The actual size is not half, but only about 85% of a normal violin size.) For such a violin, what needs to be done in order that the open strings, though shorter, sound the same notes (G, D, A, E) as on a normal violin, assuming the same strings (same mass/length) are used as on a normal violin?
   1. This cannot be done, because the a shorter string on the half violin will resonate at a smaller wavelength, hence produce sound of smaller wavelength.
   2. The tension of all the strings should be increased by equal amounts
   3. The tension of all the strings should be increased by an equal percentage
   4. The tension of all the strings should be decreased by equal amounts
   5. The tension of all the strings should be decreased by an equal percentage

7. An open tube is vibrating at its fundamental frequency. A thin flat barrier is slid into the tube sideways (perpendicular to its axis) at the center. What happens to the fundamental frequency?
   1. it increases because any additional constraint raises the resonant frequencies
   2. it decreases because the mass of the tube is increased
   3. it stays the same because we now have two closed tubes of half the length
   4. none of the above

8. The reason for the tubes underneath the bars of a vibraphone is
   1. to eliminate the anharmonic resonances of the bars
   2. to support the rotating paddles
   3. to reinforce the bars' sound when the rotating paddles allow the tube to be in resonance with the bar
   4. to make the instrument look pretty

9. In a lecture demo a horizontal metal plate, covered with fine sand, was vibrated at a high (ultrasonic) frequency. What kind of waves were generated, and how was the sand pattern related to the wave?
   1. The waves were longitudinal propagating waves, and the sand pattern showed their direction
   2. The waves were transverse propagating waves, and the sand pattern showed their direction
   3. The waves were standing longitudinal waves, and the sand settled at the nodes
   4. The waves were standing transverse waves, and the sand settled at the nodes
   5. The waves were standing transverse waves, and the sand settled at the antinodes

10. The observation that tone quality (timbre) is hardly affected at all by rather large changes in the relative phase of a tone's harmonics is summarized in
        a. Fourier's theorem           b. Helmholtz's postulate  
        c. Ohm's law of hearing      d. Gibbs phenomenon

11. In the Fourier Synthesizer shown in lecture, what feature of the synthesized wave could we not control:
        a. inharmonicities                       b. frequency of fundamental
        c. amplitudes of all harmonics     d. phases of all harmonics

12. When the Fourier spectra of two notes, each produced by a different musical instrument, are identical,
    1. The notes have the same pitch, sound similar, and the waveforms are similar
    2. The notes have the same pitch and the the waveforms are similar, but the notes can possibly sound very different to the human ear
    3.  The notes have the same pitch, sound similar, but the waveforms can possibly be very different
    4. The notes sound similar, but the pitch and waveforms can possibly be very different
    5. Sound, pitch, and waveform can all be different

13. What must be true about the Fourier spectra of two waves that, when combined, interfere completely destructively (that it, they produce zero intensity):
    1. Their spectra must consist of one single-frequency component, because they must be sine waves
    2.  Their spectra can be complex, but they must be equal to each other
    3. One wave must have only odd harmonics, the other, only even
    4. They must both have only odd harmonics
    5. They must both be symmetric waves, like sine, triangle, or square waves

14. What is the relation between a complex wave and its Fourier spectrum?
    1. The spectrum determines a unique wave shape
    2.  The wave shape determines a unique spectrum
    3. Neither determines the other
    4. Only the amplitude of the fundamental frequency is needed to define the wave, but the amplitude of all harmonics are contained in the the spectrum

15. The unique sounds occurring at the beginning of a musical sound that last for a very short time period and possess a spectrum very different from the steady note that follows are called
    a. inharmonicities       b. formants       c. attack transients       d. decay transients       e. vibrato

16. Frequency regions within which harmonics are emphasized relative to other harmonics are called
    a. inharmonicities       b. formants       c. attack transients       d. decay transients       e. vibrato

17. Periodic changes in the pitch of a musical tone are called
    a. inharmonicities       b. formants       c. attack transients       d. decay transients       e. vibrato

18. Your mouth is shaped most like a Helmholtz resonator when saying:
    a. ah       b. ee       c. oh       d. eh       e. sh

19. When saying what sound do you produce colored noise:
    a. ah       b. ee       c. oh       d. eh       e. sh

20. A child's vocal system acts like a closed tube 12 cm long. What are the frequencies of the first two formant regions? (use S = speed of sound in warm (hot?) air = 360 m/s)
        a. 1000Hz, 3000Hz       b. 500Hz, 1000Hz       c. 750Hz, 2250Hz      
        d. 1500Hz, 3000Hz       e. none of the above

21. In amplitude modulation the difference between carrier and modulator is
    1. the carrier usually has (considerably) higher frequency than the modulator
    2. the carrier is often (as in AM radio) a simple sine wave, whereas the modulator is often a complex wave
    3. the carrier generally fluctuates about an average value of zero, whereas the modulator is often offset by an amount greater than its fluctuation amplitude
    4.  all of the above

22. A simple, pure sound whose pitch "slides up" continuously from 200 Hz to 300 Hz during 0.5 sec, then drops back to 200 Hz and starts the upward slide again every 0.5 sec, can be described as
    1. a 200 Hz sine wave frequency modulated by a 2 Hz zero-offset sawtooth wave
    2.  a 250 Hz sine wave frequency modulated by a 2 Hz zero-offset sawtooth wave
    3. a 300 Hz sine wave frequency modulated by a 2 Hz zero-offset sawtooth wave
    4. a 250 Hz sine wave frequency modulated by a 2 Hz zero-offset triangle wave
    5. none of the above

23. In an analog synthesizer, the attack and decay characteristics of a sound are controlled by
    1.  the envelope generator
    2. the low frequency control oscillator
    3. the voltage controlled oscillator
    4. the amplitude modulator

Below you see a block diagram of a simple synthesizer, but instead of the usual abbreviations the blocks contain numbers. These are question numbers which you are to answer with the name of the block, using the following scheme:

True or false questions

29. The amplitude of a sound that is not at a resonant frequency of a tube is decreased when that sound propagates through the tube   T
30. A Helmholz resonator has at least three resonance peaks in its resonance spectrum   F
31. The horizontasl axis of a Fourier spectrum is time   F
32. The Fourier spectrum of a drum sound contains anharmonic frequencies   T
33. Noise is sound that contains no more than 50 different frequencies   F
34. A high pass filter removes frequencies above the filter frequency   F
35. The resonance structure of a clarinet is that of an open tube   F
36. The beep ... beep ... beep sound that indicates a truck is backing up can be synthesized by 100% amplitude modulation of a standard wave form by a square wave   T
37. A triangle wave contains higher-frequency Fourier components than a sine wave of the same frequency   T
38. Amplitude modulation produces a pure vibrato   F
39. A Fourier synthesizer is an electronic device that displays the amplitude of harmonics present in any input wave   F
40. The acoustical spectrum of a wine jug is similar to that of a Helmholtz resonator   F

This is the end of the answer sheet questions. On top of the next page, write your name legibly, and copy and sign the pledge:

Then answer questions 41-43 on that last page

41.   (3 points) Below you see drawings of a wave and of its Fourier spectrum. On the same axes, you draw
        a wave of the same wave shape, but twice the frequency, and its spectrum. Answer: red curves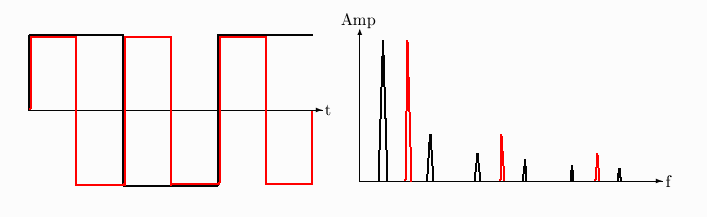
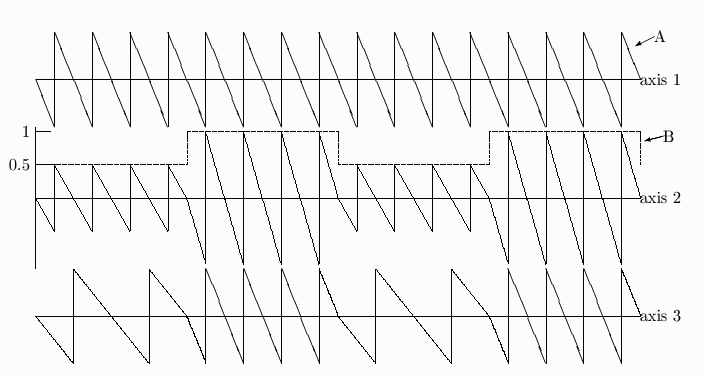
42.   (3 points) Below you see drawings of two waves, A and B. On the second axis, draw wave A amplitude
        modulated by wave B.
        On the third, empty axis, draw wave A frequency modulated by wave B.

43. (4 points) It is instructive to synthesize the sound of an instrument because in a synthesizer the "blocks" responsible for the various features of the sound are well separated. However, functions corresponding to VCO, VCA, etc. can also be identified in most actual (non-electronic) instruments (for example, some device is responsible for the pitch, analogous to keyboard and/or VCO). Pick your favorite instrument and describe in a few sentences the parts analogous to at least three blocks of a synthesizer. (Since instruments gnerally do not play be themselves, many of these "parts" will include some action of the player.) Use back of this page for answer.

    Many possible answers. One of the easier ones is the piano: the keyboard is analogous to the synthesizer keyboard. The strings taken together are the VCO (or VCO+filter if the VCO has to put out one of the standard wave forms). The pedals control various features of the envelope, for example the sustain, so they can be considered analogous to the envelope generator (but other features of the envelope, for example the decay, is due to the natural damping of the strings' vibration). The sound board acts as a filter (and amplifier, in the sense that it increases the radiated sound power compared to what it would be without the sounding board; but when present the radiated power is no larger than the power input from the strings, so it is not a power amplifier as in audio technology, it is more like an impedance matcher. Of course you were not require to give all that detail).