
(b) Around your sine wave, draw a tube (open or closed, whatever is appropriate), exactly as long as the wave, and which can contain that wave as one of its possible standing waves.
| Physics 102 |
| October 15, 2002 |
Instructions: This exam consists of two parts, Part I (written and drawn) to be answered on this sheet, Part II (multiple choice) to be answered on a ``scantron" answer sheet. Make sure you have both of these items, and mark your name (last name first) on the answer sheet. When you are finished, put this sheet in the alpabetical trays, and the answer sheet into a separate tray. You may detach this first sheet and keep the multiple-choice questions.
Part I. For these questions take the speed of sound to be S = 345 m/s.
1. (a) In the space below, draw exactly 11/2 (that is, 3/2) wavelengths of a sine wave, starting at a maximum (antinode). On your drawing, mark the distance that represents one wavelength, l. (This is meant to be a transverse representation of a longitudinal wave at one moment of time.)

(b) Around your sine wave, draw a tube (open or closed, whatever is appropriate), exactly as long as the wave, and which can contain that wave as one of its possible standing waves.
(c) If the frequency of this wave is 1000 Hz, what is its wavelength l? What therefore is the length L of the tube? (show your work!)
|
The wave crosses zero three times (3 nodes). For an open tube this means N = 3. The fundamental is therefore 1000 Hz/3 = 333 Hz
Or you could have argued:
For an open tube the fundamental has L = l/2. Since in this case, L 3l/2, we have N = 3.
2. Electrical equipment (such as radios and hi-fi equipment) runs on 60 cycle AC. Some of this voltage can leak into the audio circuits, and then causes a ``hum" of frequency f = 60 Hz in the loudspeaker. To eliminate the strong hum in his old-fashioned, monaural system, a physicist has set up the somewhat impractical but workable scheme shown below:
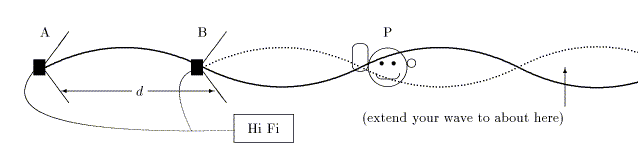
The idea is to have a second speaker B, which is being fed the same signal as the main speaker A and hence vibrates in phase with the latter, at such a distance that by the time the 60 Hz wave from A gets to the physicist P it is out of phase with the same wave from B.
(a) To start with, figure out the wavelength l of the 60 Hz sound in air.
l = S/f = (345/60) m = 5.75 m
(b) What should be the distance d between A and B so that their waves, propagating to the right, are out of phase? (if there are several possible values for d, choose the smallest such value.)Two waves are out of phase if one is shifted by l/2, so d = l/2 = 2.88 m.
(c) On the picture above, draw such waves, coming out of A and B, respectively, and propagating to the right (snapshot at a fixed time). In the region of P the waves should obviously interfere destructively, that is, add up to zero, but you draw just the separate waves.
solid curve = wave from A dotted curve = wave from B
(d) Why is it important for this scheme to work that the two waves from A and B have the same amplitude at P?
If the two waves have equal amplitudes, the cancellation is complete when the two waves are out of phase.
(e) Assume no reflections or other effects to prevent the waves from A and B spreading out equally in all directions. Note that A is twice as far away from P as B. If the output power of A is 1 watt, what should the output power of B be?
In order that the intensities at P be the same, the power of A should be 4 times that of B, by the inverse square law. Hence the power of B should be ¼ watt = 0.25 watt.
Part II Multiple Choice. Use answer sheet. Make sure you marked your name. Select the best answer, e.g., "all of the above" if each of the answers is correct.
The correct answer is indicated by bold face.
1. A millimeter (mm) is
(A) a million meters (1,000,000 meters) (B) a thousand meters (1,000 meters)
(C) a thousandth of a meter (0.001 meter)
(D) a millionth of a meter (0.000001 meter)
(E) a device to measure miles
2. Pressure is
(A) the same as Force (B) Force/area
(C) Force × area (D) Weight × area
(E) totally unrelated to Force or Weight
3. Which of the following is an example of periodic motion:
(A) A swinging pendulum, as in a grandfather clock
(B) Doing an exercise such as situps, in regular rythm
(C) The vibration of a violin string, playing a steady note
(D) The revolution of the moon around the earth
(E) All of the above are periodic motions
4. Which of the following is not necessary to have simple harmonic motion:
(A) A mass
(B) An equilibrium position
(C) Motion (that is, not a static configuration)
(D) Friction
(E) A linear restoring force
5. A relation between frequency (f) and period (T) is
(A) f = 1/T (B) T = 1/f (C) fT = 1 (D) Tf = 1 (E) All of the above
6. Two different physical quantities, having different dimensions, both undergo SHM. (For example: the electrical signal (dimension: voltage)
being fed into a loudspeaker, and the displacement of the loudspeaker cone (dimension: distance).) Which characteristics of the two SHM's cannot be compared (so it would not make sense to say, for example that the two characteristics of the SHM's are equal):
(A) Amplitude
(B) Frequency
(C) Period
(D) Phase
(E) All of the above (that is, none can be compared)
7. A tone of rapidly rising pitch (a "chirp")
(A) has a constant frequency
(B) has a constant period
(C) is not described by SHM
(D) is described by damped harmonic motion
(E) must have a rapidly rising amplitude
8. In the "beaker breaker" experiment the beaker broke because
(A) There was a strong driving force at the beaker's resonance frequency
(B) Energy was continually being transferred from sound to the beaker's vibration
(C) The force applied by the sound continually came at the proper phase with respect to the motion of the beaker
(D) The amplitude of the beaker's oscillation grew until it reached the glass' elastic limit
(E) All of the above
9. What is not true about waves:
(A) A wave is a disturbance that propagates with some finite velocity
(B) A wave transfers energy
(C) A wave always moves in some definite direction
(D) Two basic types of wave are transverse and longitudinal
(E) Examples of waves are sound waves, standing waves, ultrasonic waves, shock waves
10. The "bell in vacuum" experiment showed that
(A) the electric current to the bell gets weaker as air is pumped out
(B) sound waves require a medium - air - in which to propagate
(C) the vacuum prevents the clapper from striking the bell
(D) in vacuum our ears become insensitive to sound
(E) in vacuum, the frequency of the bell no longer resonates with that of the clapper
11. If the period of a wave is T = 1 ms, its frequency is
(A) a million hertz (1,000,000 Hz)
(B) a thousand hertz (1,000 Hz)
(C) a thousanth of a hertz (0.001 Hz)
(D) a millionth of a hertz (0.000001 Hz)
(E) the frequency cannot be determined without knowing the wave velocity
12. If the wavelength of a wave is l = 1 mm, its frequency is
(A) a million hertz (1,000,000 Hz)
(B) a thousand hertz (1,000 Hz)
(C) a thousanth of a hertz (0.001 Hz)
(D) a millionth of a hertz (0.000001 Hz)
(E) the frequency cannot be determined without knowing the wave velocity
13. A student measures the speed of 1000 Hz sound in air in a Kundt's tube. He finds the distance between nodes to be 17 cm. He calculates
|
(A) He did well, 170 m/s is about the right value for the speed of sound in air
(B) His value disagrees with the accepted value, something must be wrong with his measurement
(C) His measurement is OK, but since Kundt's tube is a "closed" tube (open only on one end), the relationship between v, f and l is different than what he used
(D) His measurement is OK, but his calculation is wrong, because from his distance between nodes it follows that the wavelength l was 34 cm.
(E) His measurement is OK because the frequency of standing waves is twice that of travelling waves, giving v = 17 ×2000 cm/s = 340 m/s, which is a reasonable value for the speed of sound in air.
14. Huygens's principle and the Superposition principle
(A) apply to all three-dimensional waves
(B) are two ways of stating the same physical idea about waves
(C) are mutually exclusive
(D) apply only to standing waves
(E) taken together imply the inverse square law for waves in any number of dimensions
15. When a sound wave enounters a solid, reflective object of size smaller than the wavelength of the sound
(A) most of the wave is reflected
(B) none of the wave is reflected
(C) most of the wave passes through the object
(D) most of the wave bends around the object
(E) the wave behind the object is 180° out of phase with the incident wave
16. The sound from a small speaker is louder and fuller if the speaker is mounted on a hole in a larger wooden board, which swerves as a baffle. This is so because
(A) the baffle prevents sound from the back of the speaker from interfering with sound from the front
(B) the baffle resonates with the sound from the speaker
(C) the rim of the speaker is held fixed, so the cone of the speaker can move with greater amplitude
(D) the baffle prevents sound coming out of the back of the speaker, so twice as much intensity comes out the front
(E) the rim of the speaker transmits oscillations to the baffle
17. When two waves of the same frequency and amplitude arrive at some location 180° out of phase,
(A) they interfere destructively
(B) they superimpose, resulting in zero sound intensity
(C) their amplitudes subtract, resulting in zero amplitude at that location
(D) their displacements add, but since one is always the negative of the other, the net effect is zero
(E) all of the above
18. When two pure waves of the same amplitude but slightly different frequencies are added,
(A) they do not interfere, the intensity of the sum is twice the individual intensity
(B) they interfere constructively, the intensity of the sum is four times the individual intensity
(C) they interfere destructively, the intensity of the sum is zero
(D) the sum alternates between constructive and destructive interference at a rate called the beat frequency
(E) the wave shape changes from sine wave to triangle wave
19. In a lecture experiment the lecturer swung a vibrating tuning fork around his head. The audience heard
(A) a steadily increasing frequency
(B) a steadily decreasing frequency
(C) constant frequency but varying amplitude due to beats
(D) increase or decrease in frequency according as the tuning fork was approaching or receding from the listener
(E) a constant frequency but varying wavelength
20. In the experiment of the previous question, the lecturer claimed that he could not hear the changes in the sound. This was because
(A) the rotating tuning fork remained at a constant distance from his head
(B) he was too close to the source of sound for the Doppler effect to develop
(C) the sound from the tuning fork was too loud
(D) the lecturer turned his head to keep the tuning fork in sight
(E) the lecturer is an old fogey whose hearing is no good
21. A listener direcly beneath a rocket that accelerates straight up hears
(A) nothing
(B) the roar of the rocket engines but no sonic boom
(C) a sonic boom as the motion the rocket breaks the sound barrier
(D) a continuous sonic boom that decreases as the rocket's distance increases
(E) rockets work only in the vacuum of outer space, hence cannot break the sound barrier
22. In a simple, one-dimensional standing wave the distance between nodes is
(A) a quarter of a wavelength (B) half a wavelength
(C) a wavelength
(D) twice a wavelength
(E) there is no relation between wavelength and distance between nodes
23. The fundamental frequency of a certain string is 100 Hz. What other frequencies are part of its overtone series?
(A) 200 Hz (B) 300 Hz (C) 400 Hz (D) 500 Hz (E) all of the above
24. A given musical interval is always obtained from two notes that have
(A) a specific difference in frequency
(B) a specific frequency ratio
(C) a specific set of overtones
(D) a specific phase difference
(E) a specific amplitude ratio
25. The fundamental frequency of a string will double if we change its
(A) length to half its original value
(B) tension to four times its original value
(C) mass per unit length to a quarter of its original value
(D) mass per unit length to half its original value and double its tension
(E) any of the above
26. The fundamental frequency of an open tube will double if we
(A) close one of the open ends
(B) double the length of the tube
(C) change the gas in the tube to one with twice the original gas' speed of sound
(D) decrease the radius of the tube to half its original value
(E) any of the above
27. The fundamental frequency of longitudinal vibration of a 2-m metal rod is 2500 Hz. The speed of sound in this metal is
(A) 2500 m/s
(B) 5000 m/s
(C) 7500 m/s
(D) 10000 m/s
(E) undetermined since the mode number, N, is not given
28. A simple harmonic motion has period 1 s. Another SHM of the same period always reaches maximum displacement 1/2 s after the first. The phase difference between the two motions is
(A) 0° (B) 45° (C) 90° (D) 135° (E) 180°
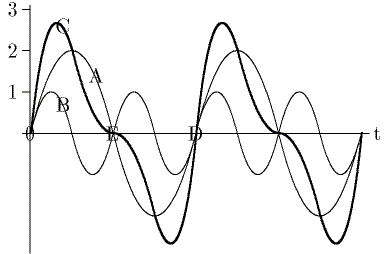
Answer questions 29-34 about the waves on the right
by marking the appropriate letter:
29. The wave of the highest amplitude C
30. The wave of the highest (largest) frequency B
31. The wave that is the sum of the two other waves C
32. The period of wave A is the distance on the t (time) axis from 0 to where? D
34. The period of wave C is the distance on the t (time) axis from 0 to where? D
35. When a wave of frequency f is added to a wave of frequency 2f, the frequency of the sum is
(A) 1/2 f (B) f (C) 1.5 f (D) 2f (E) 3f
36. On a cold day, when the speed of sound is 300 m/s, Quincke's interference experiment is done, with one tube being 0.3 m longer
than the other. What is the lowest frequency at which there will be no sound at the output (microphone)?
(A) 10 Hz (B) 90 Hz (C) 300 Hz (D) 500 Hz (E) 1000 Hz
37. A mode (in physics) is
(A) French for "fashion"
(B) one of the different oscillation patterns that are possible in a physical system that can resonate in different ways, at different frequencies
(C) a place in a standing wave where there is no motion
(D) a transverse representation of the longitudinal standing waves in a tube
(E) a fancy way of serving pie
| End of Exam |
| Hand in two items separately, with your name on both |