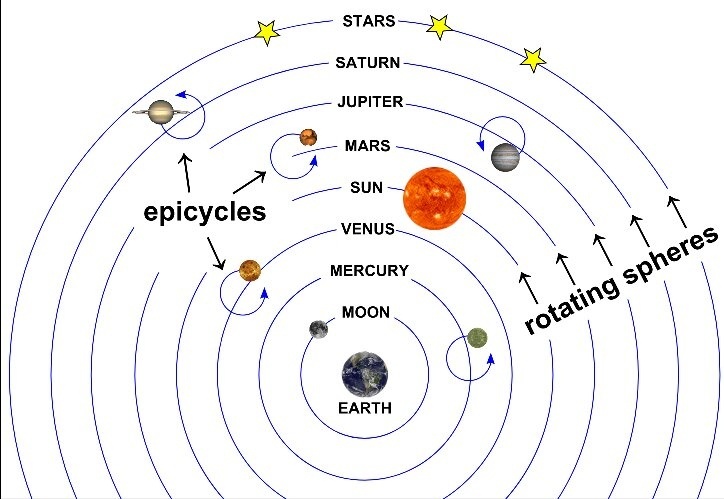
The cosmology of epicycles goes back to the 3rd century BC, and continued through Copernicus(1543) until Kepler (1561-1630). The philosophy behind is based on a religious prejudice stemming from Pythagorus and Plato coupled with early Christianity, where the cosmos are the realm of gods and thus are by definition perfect. The retrograde orbits of the outer planets, and especially Mars, which is the most eccentric of all the plants, could not be explained easily using perfect circles orbiting the earth. The way out was to introduce epicycles, which means circles upon circles. In fact, Copernicus wrote that of course the sun and all the planets orbited around the earth, but if you had everything orbit around the sun, it was easier to reproduce these orbits with epicycles. He must have almost convinced himself of the validity of the heliocentric nature of the solar system (the universe, at that time), but couldn't get past religious dogma.

Epicycles do indeed mimic the retrograde orbits of the planets as seen from earth, and look something like the following:

I remember reading in "Sleepwalkers" by Arthur Koestler how Kepler kept a notebook with details on how frustrating it was to try to get the heliocentric model to work with circular orbits, and that it took him awhile to let go of perfect circles in favor of the ellipse but that when he did, he immediately formulated his 3 laws.

In fact, if only Kepler had understood Fourier analysis, which came about around 250 years after him, he would have realized that he just needed to keep adding more and more epicycles, and tune the orbital period and radius of each circle. Because this exactly what Fourier analysis is all about: fitting functions to a sequence of orthonormal functions and tuning the amplitudes to get a good fit.

In the simulation below, hit "Start" and you will see a yellow dot orbiting with constant angular frequency about a center, and a projection of one coordinate on the right. The up and down arrow buttons allow you to add epicycles to the orbit. The radii of the orbits, and the angular frequency relative to the angular frequency about the first largest circle, are tuned to the following pattern: the main circle has a radius R, epicycle $n$ where $n=1,3,5...$ is odd, and the radius of epicycle $n$ is given by $R/n$. This is the Fourier transform of a square wave, and as you add epicycles, you can see the square wave appear.